lf243, SystemAdministration: Kriptografiye Giriş

<-- | Ana Sayfa | Erişimdüzeni | İçindekiler | Arama

Bu makalenin farklı dillerde bulunduğu adresler: English Castellano ChineseGB Deutsch Francais Italiano Nederlands Portugues Turkce

Pierre Loidreau
<pierre.loidreau/at/ensta.fr>

Yazar hakkında:

Pierre ENSTA(Ecole Nationale Supérieure de Techniques Avancées) da araştırma görevlisi olarak çalışmaktadır. Araştırma konusu "Kripto Sistemler" de hata düzeltme kodlar teoremidir. Linux ile hergün uğraşan Pierre sıksık tenis oynamaktadır.

Türkçe'ye çeviri:
Mehmet Berkay Abi <berkay_abi(at)hotmail.com>

İçerik:

Neden Kriptoloji - 2500 yıllık tarihi
AES (Advanced Encryption Standard)(Gelişmiş Şifreleme Standardı)
Genel anahtar (Public key) kriptografisi
Kriptolojinin modern kullanımı
Public (genel) veya secret(gizli) anahtar kullanımı : Farklılıkları
Kaynakça
Bu yazı için görüş bildiriminde bulunabilirsiniz

Kriptografiye Giriş

Özet:

Bu yazı ilk olarak Fransa'da yayınlanan Linux Magazine dergisinin güvenlik ağrıklı bir sayısında yayınlanmıştır. Derginin editörü, yazarlar ve çevirmenler bu özel sayıda yer alan tüm yazıları LinuxFocus'ta yayınlanmasını nazikçe kabul ettiler. Buna göre, yazılar İngilizce'ye çevirilir çevirilmez LinuxFocus'ta yayınlanacaktır. Emeği geçen herkese çok teşekkür ederim. Bu özet, diğer yazılarda aynen tekrarlanacaktır.

_________________ _________________ _________________

Neden Kriptoloji - 2500 yıllık tarihi

Kriptolojinin kökeni muhtemelen insanlığın varoluşunun başlangıçlarına, insanların iletişim kurmayı öğrenmeye başlamalarına kadar gitmektedir. İletişimlerinin gizliliğini garanti altına almak için araçlar bulmaya çalışmışlardır. Bununla beraber, mesajları şifrelemek için bilimsel methodların ilk kullanımı eski Yunanlılarla bağdaşlaştırılabilir. Tahminen milattan önce 6 yıllarında, "scytale" isimli değnek kullanmışlardır. Gönderici şerit halindeki kağıdı değnek etrafına sarar ve mesajını boylamasına bu kağıt üzerine yazardı. Daha sonra kağıdın kıvrımlarını açarak düz hale getirir ve göndereceği adrese yollardı. Değneğin genişliği (gizli anahtar gibi davranan) bilgisi olmaksızın mesajın deşifre edilmesi olanaksız olmaktadır. Daha sonraları Roma orduları iletişimlerinde Sezar 'ın (alfabede 3 harf kaydırma) şifrelemesini kullanmışlardır.

Sonraki 19 yüzyıl, çeşitli şifreleme teknikleri geliştirilmeye adanmıştır. 19. yüzyılda Kerchoffs modern şifrelemenin prensiplerini yazdı. Bu prensiplerin birisi, şifreleme sisteminin güvenilirliğinin şifreleme prosesine bağlı olmadığını, kullanılan şifreye bağlı olduğunu belirtir.

Böylece bu andan itibaren şifreleme sistemlerinin bu ihtiyaçlarla buluşması beklenirdi. Fakat varolan sistemler matematiksel altyapı ve buna bağlı olarak ölçüm araçlarından yoksunlardı. Birisi en sonunda şifrelemenin nihai hedefine erişecek ve %100 güvenli sistemi bulacaktı. 1948 ve 1949 yıllarında Claude Shannon 'un "A Mathematical Theory of Communication" ve "The Communication Theory of Secrecy Systems" isimli yazılarıyla şifrelemeye bilimsel altyapı eklendi. Bu yazılar bütün umut ve önyargıları süpürüp götürdü. Shannon, bir kaç yıl öncesine ait olan Vernam 'ın şifrelemesinin (One Time Pad olarak isimlendirilen şifreleme) varolan tek koşulsuz güvenli sistem olduğunu ispatladı. Ne yazık ki Vernam 'ın şifrelemesi de pratikte kullanışlı değildi... Bugünlerde güvenlik sistemlerinin değerlendirilmesinde sayısal güvenliğin temel alınmasının nedeni budur. Bilinmeyen saldırının zorluğu, olası bütün olası anahtarların aranmasından daha iyiyse gizli anahtar şifrelemesi güvenlidir.

AES (Advanced Encryption Standard)(Gelişmiş Şifreleme Standardı)

Ekim 2000 içerisinde, NIST (National Institute of Standards and Technology) , seçilen 15 aday arasında yeni bir gizli anahtar şifreleme standardının onaylandığını bildirdi. Yeni algoritma standardı, anahtar boyutlarının çok küçük olmaya başladığı eski DES algoritmasının yerine alacaktı. Mucitleri olan Rijmen ve Daemen 'in isimlerinden oluşan Rijndael, geleceğin gelişmiş şifreleme standardı olarak seçildi.

Rijndael, bir Blok şifrelemesinin, mesajların 128-bitlik blok parçalarıyla şifrelenmesiyle olacağını bildirir. 128, 192 veya 256 bit anahtarlar kullanılan farklı seçenekleri bulunmaktadır. DES, 56 bitlik anahtar ile 64 bitlik bloğu şifrelemektedir. Triple DES (üçlü DES) ise genellikle 112 bitlik anahtar ile 64 bitlik blokları şifrelemektedir.

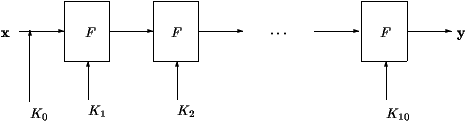
Şekil 1: AES tekrarlamaları
Geliştirilmiş şifreleme standardının (AES) işlemsel yolu Şekil 1 de gösterilmiştir. İlk olarak bir gizli anahtar K0 bit seviyesinde mesaj ile XOR işlemine tabi tutulur. Daha sonra bütün blok şifrelere, F fonksiyonu K0 anahtarından belirli bir yordam ile üretilen alt anahtarlar kullanılarak uygulanır.

AES için, F fonksiyonu 10 kez tekrarlanır.

Şekil 2, F fonksiyonunun tekrarlanma sürecini göstermektedir. 128 bitlik blok, giriş olarak alınan 16 byte'ı alır.İlk olarak S (yerine koyma) her byte için uygulanır. Daha sonra 16 byte için ikinci bir P permutasyonu uygulanır. Anahtar genişletme yordamı ile oluşturulan i 128 bitlik alt anahtar önceki sonuca bit seviyesinde eklenir.
n. tekrarın Ki anahtarı, anahtar geliştirme yordamında (n-1). tekrarda oluşan K(i-1) alt anahtarı ile K0 gizli anahtarının kullanımından elde edilir. Anahtar genişletme yordamı Şekil 3 de gösterilmiştir. K(i-1) anahtarının 16 baytı, 4 baytlık 4 parça halinde işleme alınırlar. Son 4 byte, S (yerine koyma) kullanılarak (F fonksiyonun uygulanan S) değiştirilir. Daha sonra, ilk 4 sonuç byte'ı alpha elementine eklenir. Bu element, önceden tanımlanan ve tekrar sayısına bağlı olan byte'dır. En son olarak, Ki 'yi elde etmek için 4 byte K(i-1)'in ilk 4 byte 'ına eklenir. Daha sonra sonuç diğer 4 byte'a eklenir...

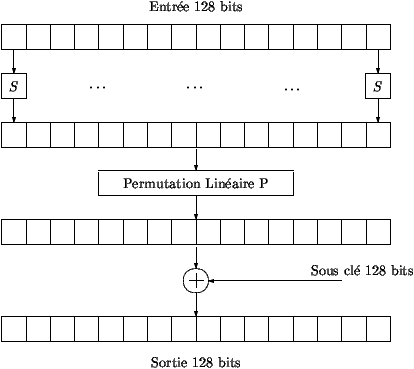
Şekil 2: F FonksiyonuF
Şimdi, yer değiştirmelerin nasıl yapıldığına ve neden aⁱ kullanıldığına kısaca bakalım. Teknik olarak (ve basit nedenlerden dolayı) bir byte, sınırlı alan denilen ve basit işlemlerin (ekleme, çarpma, ters alma gibi) yapılabildiği 256 element takımının bir elementi olarak ele alınabilir. Gerçekte, S yer değiştirmesi daha önceden ters alma olarak ifade edilmişti. S yer değiştirme, çok basit operasyon için belirlenmiş ve kolayca uygulanabilirdi. aⁱ elementi, bir elementin i kuvvetinin yüksekliğine tekabül eder. Benzer dikkat edilecek noktalar, AES 'in uygulanmasını daha verimli kılmaktadır.

AES byte bazında operasyonlar üzerine kurulmasının yanında, 2 önemli avantaj sağlamaktadır:

AES 'in katıksız yazılım uygulaması çok hızlıdır. Örneğin Pentium 200Mhz üzerinde çalışan bir C++ uygulaması, 70Mbit/s şifreleme performansı göstermektedir ;
AES 'in ayrı ve lineer şifreleme analizlerinin direnci S-Box seçimine bağlı değildir. DES için S-Box 'ların NSA için açık içerdiğinden şüphelenilmektedir. Aslında bütün operasyonlar basittir.

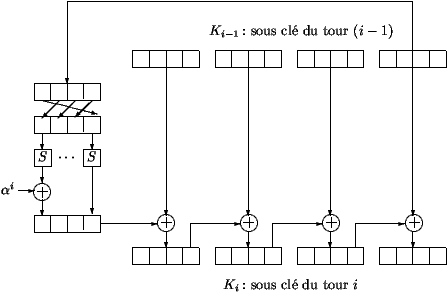
Şekil 3: Anahtar genişletme yordamı

Genel anahtar (Public key) kriptografisi

1976 yılında Diffie ve Hellman, şifrecilere gerçekten büyük kazanç sağlayan "New Directions in Cryptography" isimli bir makale yayınladılar. Bu makale genel anahtar (public key) şifreleme kavramını tanıştırmıştır. Gerçekten, o zamanlar bilinen algoritmalar (simetrik özel anahtar algoritmaları), network benzeri iletişim metotlarına girince görülen ihtiyaçları daha fazla karşılayacak gibi gözükmüyordu.

Temel olarak, yeni fikirlerinin çekirdeğini tek yönlü fonksiyonlarına açılan kapı kavramlarıyla tanıştırma vardı. Bu tür sistemler tek yönde kolayca işletilebilir, fakat fonksiyonun kendisinden geldiği herkesçe bilinen gizli tuzağı bilmeden dönüştürmek sayısal olursuz yaratıyordu. Ayrıca, genel anahtar fonksiyon gibi davranıyordu, sayılı insanın bildiği tuzak özel anahtar olarak adlandırılıyordu. Bütün bunlar, Alice ve Bob 'un dünyaya gelişini sağladı. Alice ve Bob, kendilerini dinlemeye veya iletilişimi değiştirmeye çalışanları yenerek iletişim kurmaya çalışan iki insandır.

Tabi ki, mesajın deşifre edilmesi için alıcı olan kişi gizli tuzağı kullanarak fonksiyonu dönüştürmelidir.

Genel anahtar şifreleme sistemlerine en iyi örnek (ve de en kolayı) iki sene sonra 1978 de yayınlandı. Kısaca RSA olarak adlandırılan Rivest, Shamir ve Adleman üçlüsü tarafından bulundu. Tamsayının çarpanlarına ayrılması gibi matematiksel zorluk içeriyordu. Özel anahtar, kabaca aynı boyutlardaki iki asal sayı olan p ve q ile (p-1) ve (q-1) 'a bağımlı asal d 'nin oluşturduğu (p,q,d) şeklinde üçlü bir yapıdaydı. Genel anahtar ise n=pq olan n değeri ile (p-1)(q-1) 'nin katsayısı olan d 'nin tersi olan e ye bağlı olarak (n,e) çiftinden oluşmaktaydı. ( Örneğin ed = 1 mod(p-1)(q-1)). Sözgelimi

ed = 1 mod(p-1)(q-1).

Alice'nin Bob'a yazı göndermek istediğini ve Bob'a ait genel anahtar (n,e) ile şifreleme yaptığını varsayın. İlk olarak mesajı n'den daha küçük olan bir m tamsayısı ile dönüşüm yapar,

c = m^e mod n,

ve c sonucunu Bob'a gönderir. Kendi tarafında Bob, (p,q,d) özel anahtarları ile mesajı işleme alır:

c^d mod n = m^ed mod n = m.

RSA için, tek yönlü tuzak fonksiyonu, n 'den küçük olan bir x tamsayısını x^e mod n değeriyle ilişkilendiren fonksiyondur.

RSA'dan sonra bir çok genel anahtar şifreleme sistemleri geliştirildi. Şu an RSA 'ya alternatif olabileceklerin en ünlüsü ayrık logaritmayı temel alan şifreleme sistemidir.

Kriptolojinin modern kullanımı

Gerçekten, genel anahtar şifrelemesi ilgi çekicidir, çünkü kullanımı kolaydır ve bugüne kadar çözülemeyen birçok güvenlik problemini çözmüştür. Tam olarak, bazı kimlik denetimi problemlerini çözer:

Bireyleri Tanımlama: Bugünün anonim iletişimlerini kullanma; Alice, konuştuğu kişinin kendisini aldatmadığından ve Bob'u taklit etmediğinden emin olmak ister. Böylece tanımlayıcı bir protokol kullanır. Bir çok sayıda tanımlayıcı protokol vardır ve genellikle RSA veya ayrık logaritma prensiplerine bağlıdırlar.
Döküman doğruluğu ispatı : Dijital imza sayesinde bir otorite dokümanların doğruluğu denetler. İmzalama, doküman ile otoritenin girişinin belirli işlemleri ile oluşan bir kaç bitin veya MD5 ile SHA benzeri karıştırma algoritmalarının kullanımıyla oluşan bitlerin dokümana eklenmesiyle elde edilir. Dokümana erişim yetkisi olan herhangi bir kişi, imzanın gerçekten otorite tarafından atıldığını doğrulayabilir. Bu iş için imza şemaları kullanılır. İmza şemalarının en ünlüsü Elgamal imza şemasıdır. Elgamal ayrık logaritma problemlerine dayanmaktadır.

Ayrıca, genel anahtar şifrelemesi , özel anahtar şifrelemesinde olduğu gibi şifrelemeyi, iletişimin gizliliğini garanti etmektedir.

Alice 'in Bob ile gizlice iletişim kurmak istediğini düşünün. Alice Bob'un genel anahtarını dizinden ulaşarak alır ve mesajını bu şifreyi kullanarak şifreler. Bob şifreli mesajı aldığı zaman, kendisinin özel anahtarını kullanarak mesajı çözer ve temiz mesaja okuyabilir. Her iki anahtar çok farklı rollere sahiptir, bu yüzden bu sistemlere Asimetrik Şifreleme Sistemleri denilmektedir. Şifreleme ve deşifreleme için aynı anahtarı kullanan sistemlere Simetrik Şifreleme Sistemleri denilmektedir.

Genel anahtar şifrelemesinin, özel anahtar şifrelemesine göre önemli yararı daha vardır. Gerçekçi olunursa, n kişinin özel anahtar şifrelemesini kullanması durumunda grup içerisinde her kişi için bir farklı özel anahtar ihtiyacı olmaktadır. Böylece n(n-1) adet anahtar yönetimi olacaktır. Eğer n binlerce kullanıcı olursa o zaman milyonlarca anahtar yönetimi söz konusudur... Bundan başka gruba yeni bir kullanıcı eklemesi kolay bir iş olmamaktadır, yeni kullanıcının gruptaki herkesle iletişim kurabilmesi için n adet yeni anahtar yönetimi söz konusu olacaktır. Daha sonra, yeni anahtarların gruba yollanması gerekmektedir. Aksine, asimetrik sistemlerde, kullanıcıların n adet genel anahtarları genel bir dizinde tutulur, yeni bir kullanıcı eklemesinde kullanıcının genel anahtarı dizine eklenmesi yeterli olacaktır.

Public (genel) veya secret(gizli) anahtar kullanımı : Farklılıkları

Bir önceki paragrafta genel anahtar şifrelemesinin özel anahtar şifrelemesinin çözemediği bir çok problemi çözebildiği ifade edildi. Bu noktada AES'in neden düzenlendiği merak edilebilir. Bu tercihin iki temel açıklaması vardır;

İlki pratik bir sebeptir. Genel olarak genel anahtar şifrelemesi çok yavaştır. Örneğin, RSA 'nın yazılım uygulaması AES 'e nazaran binlerce kat daha yavaştır ve RSA donanım uygulaması için dizayn edilmemiştir. Bilgi gönderimi bugün için çok kritiktir, şifreleme algoritmasınca oluşan bir sınırlama kabul edilemez.
İkincisi, genel anahtar şifrelemesinin dahili yapısı diğer güvenlik problemlerine neden olmaktadır.
Örneğin, genel anahtar şifreleme sistemleri, özel anahtar sistemlerine nazaran daha geniş anahtar boyutları gerektirir. Gerçekte, özel anahtar şifreleme sistemlerinde anahtar uzunluğuna önem verilmektedir. Bu nedenle, bu sistemlerin kaba kuvvet saldırıları ile yenilebileceği görülmektedir. Örneğin bütün oalsı anahtarların numaralandırılması... Eğer anahtar uzunluğu 128 ise 2¹²⁸ numaralandırma olmaktadır.
Fakat genel anahtar şifrelemesinde, anahtar boyutu aynı sistem düşünüldüğü zaman ilgiye değer bir parametre olmaktadır. Örneğin, 512 bitlik anahtara sahip RSA, 128 bitlik anahtarlı AES'e göre daha güvensizdir. Genel anahtar şifrelemesini doğru olarak hesaplayabilmenin tek yolu, en iyi bilinen saldırıyı hesaplamaktır ve bu biraz farklıdır: Yeni bir buluşun sistemin güvenliğiyle uyuşacağını kimse bilemez. Son zamanlarda, bir grup araştırmacı 512 bit tamsayıyı çarpanlarına ayırdı. Sonuç olarak 1024 bit tamsayılar kullanımı en doğru güvenlik seviyesi için doğru olacaktır.

Sonuç olarak, şifreleme için mümkünse özel anahtar algoritmaları tercih edilir. Zimmermann ilginç bir hibrit çözüm üzerine çalıştı. Temel olarak, Alice ve Bob bütün özellikleri ile özel anahtar algoritmasıyla iletişim kurmak istediklerinde;

Alice ve Bob, bir anahtar değişim protokolü kullanarak özel anahtar için anlaşıyorlar. Anahtar değişim protokolleri genel anahtar şifrelemesi kullanmaktadır. En ünlü protokollerin birisi, Diffie-Hellman'ın algoritmasına dayanmaktadır.
Daha sonra onlar IDEA algoritması ile iletişim kurarlar.

İletişimi tamamladıklarında, üzerinde anlaşılan oturum anahtarı atıldı. Böyle bir sistem, hem genel anahtar şifreleme sistemlerini hem de genel anahtar şifreleme sistemlerini kullanır. Genellikle bunun gibi sistemlerin en güvensiz parçasının anahtar değişim protokolü olduğu düşünülür.

Kaynakça

Şifreleme Tarihi :

S. Singh : Histoire des codes secrets. Jean-Claude Lattès, 1999.
D. Kahn : The Codebreakers: the story of secret writing. MacMillan publishing, 1996.

AES için :

Genel Şifreleme:

Article of Anne Canteaut and Fran Lévy-dit-Véhel : http://www-rocq.inria.fr/canteaut/crypto_moderne.pdf
B. Schneier : Applied Cryptography. John Wiley and Sons, 1996.

Bu yazı için görüş bildiriminde bulunabilirsiniz

Her yazı kendi görüş bildirim sayfasına sahiptir. Bu sayfaya yorumlarınızı yazabilir ve diğer okuyucuların yorumlarına bakabilirsiniz.

talkback page

<--, Bu sayının ana sayfasına gider

Çeviri bilgisi:

fr --> -- : Pierre Loidreau <pierre.loidreau/at/ensta.fr>

fr --> en: Axelle Apvrille <axellec/at/netcourrier.com>

en --> tr: Mehmet Berkay Abi <berkay_abi(at)hotmail.com>

2004-01-10, generated by lfparser version 2.45