
by Pierre Loidreau
<pierre.loidreau(at)ensta.fr>
关于作者:
Pierre是法国ENSTA (Ecole Nationale Supérieure de Techniques Avancées)里的一个教师和研究人员。他的研究领域是关于基于纠错码理论的密码学。他每天”玩”Linux..还有经常打网球。
目录:
|
密码学简介

摘要:
这篇文章首先登在法国的一本linux杂志的一期关于安全的特刊上。编辑,作者以及翻译人员好心的允许LinuxFocus杂志刊登这个特刊里的任意一篇文章。所以只要这些文章被翻译好了,LinuxFocus杂志就会尽快地呈现给读者。谢谢所有参与这项工作的人。如果所有文章都是来自这个特刊的话,都会使用这个摘要。
为什么要进行加密?--2500年的历史
密码学的起源可能要追溯到人类刚刚出现,并且尝试去学习如何通信的时候。他们不得不去寻找方法确保他们的通信的机密。但是最先有意识的使用一些技术的方法来加密信息的可能是公元六年前的古希腊人。他们使用的是一根叫scytale的棍子。送信人先绕棍子卷一张纸条,然后把要写的信息打纵写在上面,接着打开纸送给收信人。如果不知道棍子的宽度(这里作为密匙)是不可能解密里面的内容的。后来,罗马的军队用凯撒密码(三个字母表轮换)进行通信。
在随后的19个世纪里面,主要是发明一些更加高明的加密技术,这些技术的安全性通常依赖于用户赋予它们多大的信任程度。在19世纪Kerchoffs写下了现代密码学的原理。其中一个的原理提到:加密体系的安全性并不依赖于加密的方法本身,而是依赖于所使用的密匙。.
那么,从这个角度来看,加密体系应该能够满足那些需求的。可是,当时的加密体系仍然缺少数学的背景,因而也缺少测量或评价这些体系抗攻击的能力。要是有人能最终达到密码学的终极目标,即找到百分百无条件安全的体系那该有多好呀!在1948年和1949年,香农(Claude Shannon)在他的两篇论文里,把科学背景加入了密码学。这两篇论文是《通信的数学原理》以及主要的《秘密体系的通信原理》。那些文章把许多的希望和偏见都扫开了。同时香农(Claude Shannon)还证明了Vernam密码(也称为One Time Pad)是当时唯一无条件安全的体系。不幸的是,那个体系在使用上是不可行的...。这就是为什么现在评价体系的安全性相反是基于理论上计算得到的安全性的理由。如果还没有找到一种比完全搜索可能的密匙值这种方法更好的攻击方法的话,你可以说这种密匙加密方法是安全的。.
AES(高级加密标准Advanced Encryption Standard)
2000年10月,NIST(美国国家标准和技术协会)宣布通过从15种侯选算法中选出的一项新的密匙加密标准。新的标准将会代替密匙长度变的太短的旧的DES算法。Rijndael被选中成为将来的AES。Rijndael这个名字是从它的两个发明者Rijmen和Daemen的名字得来的。
这个加密体系据说是一种分组加密方法,因为信息的内容是以128位长度的分组为加密单元的。加密密匙长度有128,192或256位多种选择。正象你所知的那样,DES加密的分组长度是64比特,而密匙长度只有64比特。三重DES加密的分组长度通常是64比特,而密匙长度上112比特。
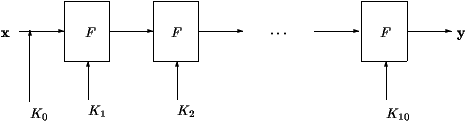
表一: AES 迭代
图一描述了AES的操作模式。首先密匙K0和待加密信息按位相与。然后所有要加密的分组都用一个函数F进行迭代计算,计算用的子密匙是由一个密匙扩展函数产生的,初始的密匙是主密匙。
对于AES 函数F要迭代10次。
- 图2描述的是加密过程中函数F是如何被迭代的。一个128位的分组转换成16个字节,作为下面处理的输入。首先,每一个字节分别经过替换函数S的处理,然后,用第二个置换函数P对16个字节进行处理。然后这个结果就和匙扩展函数产生的子匙进行位与。
- 匙Ki是用匙扩展函数从第K(i-1)轮的子匙和第K0的密匙得到的。图三描述了匙扩展函数。16个字节的被分成4组,每组4个字节,来进行处理。最后的一组的4个字节由替换函数S(这个S和用F函数进行迭代处理时的S是一样的)来进行替换处理。最初的4个字节的结果和α系数相加,这个系数是与轮数相关的,它是预先定义的。最后,为了得到Ki,把得到的4个字节的结果和K(i-1)匙的最初4个字节按位相加,然后得到的结果又和K(i-1)匙的下面的4个字节按位相加,如此类推。
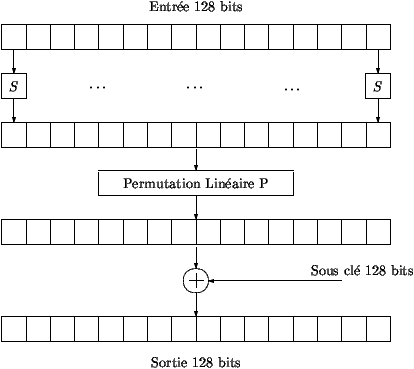
表2: 函数 F
好了,现在我们简单地看看替换函数是怎么得到的,然后看看ai 常数有什么作用。为了简单的理由,一个字节应该是256个元素集(称为有限域)的一个元素,对于这些元素只包含一些简单的操作(例如加法,乘法,反转)。事实上,前面提到的替换函数S在那个有限域里的反转。置换函数S被定义为一个很简单的操作,以便能简单的实现。ai 系数是和指数I(有限域的元素)成正比的。这些考虑,使得AES实现起来非常有效。
因为AES仅仅在基于简单的位操作运算,这有两个主要的优点:
- 即使是纯粹的软件实现,AES也是很快的。例如,用C++在奔腾200的电脑上实现的AES的加密速度可达到70M位/秒;
- AES并不依赖于S-Box的选择(根据NSA, DES里的S-Boxes可能包含后门),对分析算法抗击差分密码分析及线性密码分析具有能力。
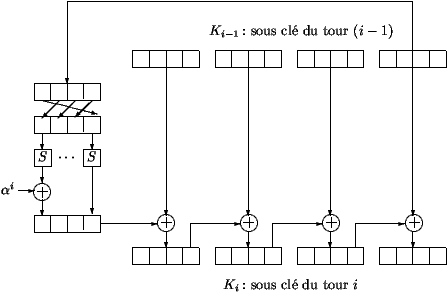
表 3: 匙扩展例程
公匙加密
在1976年,Diffie 和Hellman发表了一篇叫《密码学新动向》的文章,这篇文章给密码学社区的研究者带来了很大的轰动。这篇文章介绍了公匙加密的概念。实际上,作为当时所知道的唯一的一种算法-对称密匙算法-已经不能满足由于网络等的通信手段而引起的通信量急增的需要
基本上说来,他们的高明想法的核心就是单向函数的机关。对于那个函数来说,一个方向上的操作是容易的,但是如果不知道秘密的机关,即使所有人都知道函数本身,从反方向计算是不现实的。在这里,公匙的扮演的角色和函数相同,仅被有限的一部分人知道的机关就是私匙。这样,爱丽斯和鲍勃(以及其他人)的世界就诞生了。爱丽斯和鲍勃是两个希望进行具有完整性要求的通信的人,他们需要防止有人监听和篡改通信。.
不用说,接收信息的人要使用私匙,逆向使用函数,来解密信息。
公匙体系最好(当然也是最简单的)例子在两年后,也就是1978年出现了。它是由Rivest, Shamir 和Adleman发明的,所以也被称为RSA。RSA算法建立在对整数的分解的数学难题上的。私匙是由三个数(p,q,d)组成,其中p和q是两个素数(具有大致相同的大小),而d和(p-1)*(q-1)互质。公匙由两个数(n,e)组成,其中n=pq,而e是(p-1)(q-1)取d为模的倒数,
例如:
ed = 1 mod(p-1)(q-1).
假如爱丽斯想鲍勃的公匙(n,e)加密,传送一些文本。她首先会把明文转换成小于n的整数m,那么她就会这样处理:
c = me mod
n,
然后把结果c送给鲍勃。在鲍勃的这边,他就会用他的私匙(p,q,d)进行这样的处理:
cd mod n =
med mod n =
m.
对于RSA,单向的机关函数是能够从一个小于n的整数x得到xe mod n.
从RSA产生以来,又发明了许多其它的公匙体系。现在来说,除了RSA外,其中一个还可选择的最有名的体系是基于离散算法的。
密码学在现代的应用
实际上,公匙加密由于更容易的使用,以及能解决了目前为止许多安全的问题,所以更为吸引人。说的更准确点的说,它解决了一些认证的问题:
- 身份认证: Alice在使用今天的匿名通信的时候,她想肯定她正在通信的对象并不是假扮Bob的。为了达到这样的目的,她使用了一个认证协议。现在有许多认证协议的存在,通常都是基于RSA或离散对数原理的。
- 文档认证::一个授权机关通过一个数字签名来认证一个文档。签名通常附加在消息后面,这些签名通常是把文档和授权机关的一些信息作为输入而得到的一些字节位,这些得到的签名通常是通过MD5或SHA等的哈希算法hash得到的。还有就是, 任何访问该文档的人都应该能够去检查签名是否真的由授权机关签发的。为了实现这个目的,使用了所谓的签名模板(signature schemas)。其中一个最有名的模板是ElGamal模板,又是基于离散算法问题的。
此外,与密匙加密相比,公匙加密还提供基于密码的加密体系,以确保通信的保密性。
此外,与密匙加密相比,公匙加密还提供基于密码的加密体系,以确保通信的保密性。
我们想象一下爱丽斯想和鲍勃进行秘密的通信。爱丽斯从一个公共的目录里取得鲍勃的公匙,然后他用这个公匙对他的明文进行加密。当鲍勃接收到了密文,他就用他的私匙对密文进行解密,得到信息的内容。这些匙各起着很不同的作用,这就是为什么这些体系被称为不对称加密体系的理由。与此不同,密匙加密体系的加密和解密用的都是相同的匙,所以就被称为对称加密体系。
公匙加密与密匙加密相比,还有另外一个更为突出的优点。实际上,如果有N个用户需要通过密匙加密体系进行通信的话,每一个人和组里的任何一个人通信都需要不同的密匙,就是说,需要管理N(N-1)条密匙。如果N是上千的话,就会有上百万的密匙需要管理...。更糟糕的是,即使是增加一个用户也并非是一个简单的任务,因为为了使这个用户和组里的所有成员通信,需要产生N个新匙,然后那些新匙都要送遍整个组。与此相反,在非对称加密体系里面,成员的N个公匙是存放在一个公共的目录里面,新增一个新用户要做的只是简单的把他的公匙添加到目录里面就是了。
使用公匙还是密匙--找出合适的方案
前面的章节已经说明了公匙加密可以解决很多密匙加密不能解决的问题。有很人和疑惑:那AES还有什么作用呢?实际上,对于这种选择有两个主要的理由:
- 首先是实用上的理由。一般来说公匙加密体系是很慢的。例如RSA的软件实现比AES慢一千倍,还有RSA并不为硬件实现而设计的。在传递信息这么苛刻的今天,我们是不能接受被一个加密算法而限制的。
- 其次,公匙加密体系的内部结构导致了其他的安全问题。
例如,对于一个特定的安全水平,公匙加密体系要求匙的长度比密匙加密体系的匙的长度大的多。实际上,对于匙的长度的重要性和观念,仅仅是对于密匙加密体系才有意义。事实上,那些体系依赖于这样的事实:只有野蛮的攻击才可能攻破他们,例如,穷举所有可能的匙值,如果匙的长度是128比特的话,那么2128 个匙值需要被穷举。
但是对于公匙加密体系,仅仅在考虑相同的体系的时候,匙的大小才是一个有意义的参数。例如,匙的长度是512比特的RSA的安全性比匙的长度是128比特的AES差。正确地评估一个公匙加密体系的唯一办法是估计一些众所周知的攻击方法的复杂性,这样一来的话,事情就完全不同了:你永远不知道是否有新的办法破坏体系的安全性。最近,一组研究人员成功的把一个512位的整数分解因子。所以对于一个合理的安全水平,通常建议用1024位的数字。
所以,对于纯粹的加密来说,当能使用密匙加密算法的时候,优先使用密匙加密算法。Zimmermann已经研究了一个有意义的混合的方法,这个方法在PGP里实现。大致说来,当爱丽斯 和鲍勃 想进行具有完整性特征的通信的时候,使用一个密匙加密算法(PGP用的是IDEA):
- 首先爱丽斯 和鲍勃使用匙交换协议来协商一个密匙。匙交换协议用的是公匙加密。其中最著名的一个协议是基于Diffie-Hellman的算法的
- 然后他们用IDEA算法进行通信。
当他们完成通信以后,协商到的会话匙就会被丢弃。那样的一个系统即使用了密匙加密体系也使用了公匙加密体系。通常,大家认为这样一个体系里,比较不安全的部分是匙交换协议。
参考文献
密码学的历史:
- S. Singh : Histoire des codes secrets. Jean-Claude
Lattès, 1999.
- D. Kahn : The Codebreakers: the story of secret
writing. MacMillan publishing, 1996.
对于AES :
密码学综述 :
对这篇文章发表评论
每篇文章都有各自的反馈页面。在这个页面里,您可以提交评论,也可以查看其他读者的评论:
2002-05-28, generated by lfparser version 2.27




