![[Top bar]](../../common/images/Topbar-de.gif)
![[Bottom bar]](../../common/images/Bottombar-de.gif)
![[Photo of theAuthor]](../../common/images/Antonio-C.gif)
von Antonio Castro
Über den Autor:
Computer-Wissenschaft
ist mein Beruf und auch Teil meiner Freizeit. Ich teile gern mein Hobby,
wie es vermutlich jeder macht. Ich gebe es zu! Ich bin einer dieser seltsamen
Charaktere, die Windoze nicht mögen, sogar MS-Dos fällt
in die Kategorie eines Spielzeugs, es stellt geringste Ansprüchean
deine Fähigkeiten und füllt deinen Computer mit vielzähligen
Dateien, von denen man nicht weiß, ob sie nützlich oder wozu
sie gut sind.
Inhalt:
|
Design rekursiver Strukturen
![[Illustration]](../../common/images/illustration11.gif)
Zusammenfassung:
Hier untersuchen wir, wie man rekursive (wiederkehrende) Strukturen mit
POVRAY entwerfen und schöne Bilder mit dieser Technik erstellen
kann.
Kunst und Technik der Informatik.
Unsere Artikelserien zu POVRAY berichten über technische und nichttechnische
Aspekte von POVRAY. Technologie ist wichtig, wir bemerkten es bereits einige
Male, doch es ist wichtiger zu lernen, ihre Möglichkeiten
auch im künstlerischen Bereich zu nutzen.
Die Informatik ist nicht wie andere Disziplinen, die vielleicht für
Einige die perfekte Umgebung zum Darstellen seiner oder ihrer künstlerischen
Fähigkeiten sein können. Wir sollten auf jeden Fall etwas über
die Technologie lernen, denn es ist ein unerlässlicher Schritt, jedoch
ist in meiner persönlichen Sichtweise Technologie nur ein Instrument,
das uns hilft, eine neue Form der Kommunikation zu erreichen. In
meinen Artikeln versuche ich rein technisches Wissen mit
Kreativität und Kunst zu mischen. Mein Ziel sind fortschrittliche
Ideen, Beispiele, die die Vorstellungskraft auslösen und vielleicht
neue Wege im Geist der Leser eröffnen können. Manchmal beginne
ich mit der Gestaltung eines neuen Beispiels und ich habe so viel Spaß,
dass das Ergebnis, das ich bekommen wollte in Vergessenheit geriet. Eine
rein systematische Präsentation wird langweilig und daher nicht sehr
lehrreich. Die Documentation zu Povray wurde als eine systematische
Präsentation verschiedener technischer Ergebnisse entwickelt und
ich nutze sie gerne als Referenz.
Im Gegensatz dazu
werden wir in dieser Anleitung mehr einer spiralförmigen Annäherung
folgen, vielmals zurück zum gleichen Ergebnis kommend aber mit immer
größerer Tiefe. Die in unseren Beispielen vorgestellten
Szenen, dienen nicht nur zu Illustration der technischen
Ergebnisse, sondern auch als ästhetische Beispiele,
wie diese besondere Technik genutzt werden kann, um ein schönes Resultat
zu erhalten.
Dieses Ziel kann erfordern, daß neue und fremde Elemente
von Povray vorgestellt werden, die noch nicht in unserer Serie besprochen
wurden. Bitte nicht aufregen, wenn man nicht alles gleich versteht, Schritt
für Schritt werden wir jeden Punkt in den Beispielen erklären.
Andererseits sind viele genutzte Techniken von Natur aus anschaulich,
bereits das
"Sehen" der Resultate in den Beispielen ist dann oft mehr wert als eine lange
Erklärung.
Diejenigen, die wirklich schnell Povray lernen wollen können immer
zum Povrayhandbuch greifen.
Einfache geometrische Objekte
Die meisten der Objekte wurden bereits in vorherigen Beispielen verwendet.
Lasst uns zunächst dahin zurückblicken, um all diese Informationen
zusammenzutragen. Die Zahl der Objekte, die auf den folgenden einfachen
geometrischen Objekten basierend entworfen werden können, ist unbegrenzt,
deshalb reduzieren wir die Objekte zu einer Gruppe elementarer Formen,
was eine erhebliche Zeiteinsparung bei der Herstellung von Szenen ergibt.
Hier ist unsere Aufstellung:
- Kugel (sphere)
syntax: sphere { < x, y, z>, radius ... }
wobei x, y, z die Koordinaten eines Mittelpunktes sind. Nach dem Radius
können zusätzliche Anweisungen zur Spezifikation anderer Charakteristiken
wie Maßstab(scale), Rotation(rotation), Verschiebung(translation),
Textur(texture), Farbe(color) usw. folgen.
- Kegel (cone)
syntax: cone { <x1, y1, z1>, rad1 <x2, y2, z2>, rad2 [open] ..... }
Diese Anweisungen spezifizieren einen Kegelabschnitt , x1, y1, z1 sind die
Koordinaten des Kegelmittelpunktes am einen Ende und r1 der Radius dieses
Abschnittes und x2, y2, z2 und r2 sind die Mittelpunktkoordinaten und der
Radius am anderen Ende. Um einen reinen Kegel herzustellen, benutze man
erst einen Radius gleich null. Ein anderer erlaubter Parameter ist das
symbolische "open", ist es vorhanden wird ein offener Kegel gerendert,
wenn nicht, ist der Kegel geschlossen.
- Zylinder (Cylinder)
syntax:cylinder { <x1, y1, z1>,
<x2, y2, z2>, rad [open] ...... }
wobei x1, y1, z1 und x2, y2, z2 die Mittelpunktkoordinaten des Zylinders
an beiden Enden sind. Wie vorher ist rad der Radius um den Mittelpunkt
dieses Zylinderabschnitts und das Zeichen "open" ein zulässiger Parameter,
um einen offenen oder geschlossenen Zylinder zu unterscheiden.
-
Fläche (Plane)
syntax:plane { <x, y, z>, dist ..... }
Diesmal geben x, y und z nicht die Koordinaten eines Punktes an,
sondern die Vektorsenkrechte zur Fläche. Der Wert dist ist der Abstand
vom Koordinatenzentrum zur Fläche. Zur Erinnerung, Povray erlaubt
eine Abkürzung der Vektoren wie bei x = <0, 1 , 0> -z = <0, 0, -1.>
Manchmal kann eine Fläche unter Nutzung eines sehr großen Radiuses
dargestellt werden; tatsächlich nutzten wir diese Technik in einem
früheren Artikel.
- The Box
syntax: box { <x1, y1, z1>, <x2, y2, z2>...... }
hier sind x1, y1, z1 and x2. y2. z2 die Koordinaten der gegenüberliegenden Ecken des Kastens.
Constraint Solid Graphics(CSG) [zusammengesetzte einfache Grafiken]
CGS Primitive sind elementare einfache Objekte, die zu komplexeren Modellen
kombiniert werden können. Die abgeschlossene Kombination kann unter
Nutzung von Maßstab, Verschiebung, Rotationsverschiebung oder Texturierung
usw. gruppiert und geändert werden. Es ist nicht nötig, jede
dieser Änderungen für jede dieser elementaren Primitiven im kombinierten
Modell anzuwenden. Es gibt vier Methoden, CGS Primitive zu kombinieren,
und es gibt eine fünfte ergänzende Methode, die auf einzelne
Primitive angewandt wird:
-
Vereinigung (Union)
'union { object {A} object{B} }'
Alle Punkte im kombinierten Objekt gehören zu A oder B
-
Schnittmenge (Intersection)
'intersection { object {A} object {B} }'
Alle Punkte im kombinierten Objekt gehören zu A und B.
-
Umkehrung (Inverse)
object {A inverse}
Alle Punkte im kombinierten Objekt gehören nicht zu A.
-
Differenz (Difference)
'difference { object {A} object {B} }'
Alle Punkte im kombinierten Objekt gehören zu A doch nicht zu B,
mit anderen Worten 'union { object {A} object {B inverse }'
-
Mischung (Merge)
'merge { object {A} object {B} }'
wie in der Vereinigung, außer wenn die inneren Oberflächen von A und B
entfernt wurden. Sind die Objekte undurchsichtig, sind diese Merkmale
nutzlos.
In den folgenden Beispielen werden wir verschiedene dieser Operationen
zum Bau einfacher Modelle nutzen. Ich empfehle die Modelle zu bauen,
indem man zuerst alle die Elemente hinzunimmt, die man für das Gesamtvolumen
benötigt, und dann die Schnittpunkt-Operationen benutzt, um die unerwünschten
Teile zu entfernen.
#define EatenApple = intersection {
object { WholeApple }
object { Bite1 inverse }
object { Bite2 inverse }
}
Wenn primitive Objekte in einem einfachen Modell eine gemeinsame Oberfläche
haben, kann es in der einen oder anderen Oberfläche beim Rendern der
Punkte Probleme geben, entsprechend der Genauigkeit der Maschine. Diese
Probleme können beseitigt werden durch eine sehr kleinen Verschiebung
in einem der Objekte, um klar zu stellen, zu welchem Objekt die Oberfläche
gehört.
Schleifen und Bedingungen in Povray.
Die Elemente in einer Szene werden generell in ungeordneter Reihenfolge
beschrieben. Trotzdem gibt es Gründe, wenn es sehr bequem ist, z.
B. verfahrensgerechte Schleifen durchzuführen, um sich wiederholende
Strukturen zu gestalten. Schleifen können in Povray unter Nutzung
mehrerer Methoden durchgeführt werden. Eine Methode ist die Schleifenflusskontrollanweisung(loop
flow control directive) vorgesehen durch die Sprache selbst. Die
Schleifenflusskontrolle ist nur eine von vielen Anweisungen auf der Povray
Programmierungsoberfläche. Vor einer Weile erwähnten wir andere
Anweisungen wie #declare und #include und wir charakterisierten viele andere
mit geringerer Wichtigkeit. Das folgende Beispiel wurde direkt in Povray
bearbeitet und ich muss zugeben, ich habe die Schleifenflusskontrollanweisung
zum ersten Mal benutzt. Der Grund ist, dass es oft möglich ist, die
gleichen Resultate durch das Erzeugen der Povray-Quelle mit einem anderen
Programm (C oder C++), das Schleifenflusskontrollbefehle (für Schleife)
besitz zu erreichen. Wir werden an einigen Punkten ein Beispiel dieser
Technik sehen. Der Leser mit C-Erfahrung wird verstehen, dass Povrays
Programmieroberfläche nicht so elegant ist, wie die andere allgemeingültiger
Programmiersprachen (C, C++). Das sollte keine Überraschung sein,
weil Povray als eine Sprache zur Beschreibung von Szenen entworfen und
die Flusskontrollanweisungen später hinzugefügt wurden. Ähnlich,
der POVRAY Anweisungen zur Ausführung komplexer mathematischer Operationen
und jeder Art von Schleifen. Persönlich meine ich, es ist fantastisch,
dass POVRAY all diese Operationen beinhaltet, andererseits sind sie nicht
wirklich notwendig, seit wir sie überall in externen stärkeren
Programmiersprachen ausführen können. Ich verstehe nicht, wie
die Ausführung dieser Operationen extern oder intern einen Unterschied
für den abschließenden künstlerischen Wert der Komposition
macht. Für mich ist die Qualität des fertigen Bildes das wichtigste
Thema. Für ein geringeres Maß sollte es auch ein Faktor der
benötigten Zeit und Aufwand zur Entwicklung und Bearbeitung des Bildes
sein. Anwender, die sich in allgemeingültigen Programmiersprachen
besser auskennen, würden lieber damit POVRAY-Dateien erstellen, andere,
ohne Programmierkenntnisse, finden es vielleicht besser, direkt in Povray
zu schreiben. Auch ist es für einfache Bilder leichter, sie in Povray
zu editieren, während die Erstellung von Povray-Dateien für komplexe
Szenen durch andere Programme besser sein könnte. Wir werden beide
Methoden untersuchen und den Leser schlußfolgern lassen.
Nutzen der Trial and Error Methode [ Versuch und Fehler ]
Viele Szenen können aus einer einfachen Idee heraus entworfen werden.
Nach einer ersten Ausführung können wir uns dafür entscheiden,
einige Werte zu ändern oder Annäherungen zum Erreichen eines
besseren Resultats zu nutzen. Somit ist Trial und Error ein integrativer
Teil des Szenenentwurfs in POVRAY. Am Anfang dieser Artikelserien
boten wir den Lesern ein einfaches script-tool (POV) zur Erleichterung
des Bildaufbaues, doch der Leser sollte nicht denken, dass dieses kleine
Script ausreichend ist. Oftmals wirst Er ein Blatt Papier, Stift und Taschenrechner
brauchen. Bei vielen Gelegenheiten hat man keine Wahl, weil unsere Entwürfe
3D Geometrien betreffen, einiges Wissen über Spezialgeometrie und
Trigonometrie sind fundamentale Voraussetzung um bestimmte Effekte zu erhalten.
Generell ist es ausreichend, einige Formeln zu kennen, so lasst uns einiger
grundlegender trigonometrischer Verhältnisse erinnern:
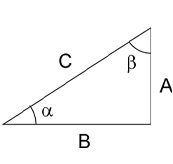 sin(a) = A / C = (gegenüberliegende Seite / Hypothenuse)
sin(a) = A / C = (gegenüberliegende Seite / Hypothenuse)
cos(a) = B / C = (benachbarte Seite / Hypothenuse)
tan(a) = A / B = (gegenüberliegende Seite / benachbarte Seite)
daraus folgt::
A = sin(a)/C
B = cos(a)/C
C = sqrt(A^2 + B^2)
da 2* Pi im Bogenmaß = 360º
1 Radian = 180 / Pi = 57,29577951308232
1º = Pi / 180 = 0,174532925199432957
Als Gedächtnisstütze werden wir zunächst das Hauptfeld der
trigonometrischen Funktionen als eine Funktion des Quadranten tabellieren:
| Quadrant |
Sinus |
Cosinus |
Tangens |
| 0 .. 90 |
0 .. +1 |
+1 .. 0 |
0 .. +unendlich |
| 90 .. 180 |
+1 .. 0 |
0 .. -1 |
-unendlich .. 0 |
| 180 .. 270 |
0 .. -1 |
-1 .. 0 |
0 .. +unendlich |
| 270 .. 360 |
-1 .. 0 |
0 .. +1 |
-unendlich .. 0 |
a = atan(A/B)
Das letzte Verhältnis ist nicht einmalig definiert. Der Winkel
alpha ist unbestimmt bei +/- 180 Grad. Zur Berechnung sollte man besser
folgendes nutzen:
a = atan2(A,B) Schließlich
ist der Abstand von P1(x1,y1,z1) zu P2(x2,y2,z2)
D = Wurzel aus( (x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2 ) Es gibt viele
nützliche trigonometrische Verhältnisse, doch ein bereits überprüftes
sollte für die meisten Fälle ausreichend sein. Die impliziten
trigonometrischen
in POVRAY ausgeführten trigonometrischen Funktionen erwarten Winkeln
in Radianten anstelle von Winkelgraden. Die Umwandlungsfunktion radians(alpha)
wandelt Grade in Radianten um. Leider ist POVRAY nicht konsistent, z. B.
werden Rotationen in Grad gemessen! :-(
Seeigel
Im folgenden Beispiel benutzen wir eine sehr grundlegende Trigonometrie.
Die Stacheln des Seeigels sind sehr ästhetisch plaziert, und dieser
Effekt kann nicht einfach durch Zufall erreicht werden. Der Entwickler
muss an einen Algorithmus entwickeln, um die Stacheln exakt zu plazieren
und diesen mit einer klaren Vorstellung der fertigen 3D Konfiguration
ausführen. Der Quellkode für das Beispiel ist ausreichend dokumentiert,
so ist es nicht schwer, hier spätere Kommentare zu machen. Dieses
Beispiel ist ein klarer Fall wo ein Umlaufalgorithmus angelegt ist. Es
ist ein Gegenstand der persönlichen Wahl ob der Entwickler sich entscheidet,
eine Schleife in POVRAY anzulegen, oder außerhalb via einem C-Programm.

Hier sind die Quellen für den Fisch. Sie sind mit CGS Primitiven
gestaltet wie vorher beschrieben.
balistap.inc
Als nächstes kommt die Quelle für den Rest der Szene. Das einzige
Thema hier ist die Definition des Seeigels (erizo in spanisch), der ohne
einen Zweifel der grundlegendste Charakter dieser Komposition ist:
erizo.pov
Eine Anzahl von Effekten in diesem Beispiel sind komplett neu, z. B. die
Oberflächeneffekte auf dem Sand (Wellen auf dem Sand), die athmosphärischen
Effekte (ein Nebel aus grauer Marinefarbe sehr dick und feucht) sowie die
komplexen CGS Objekte. Das Licht in dieser Szene kommt von vielen Punktquellen,
über das Medium verstreut, zur Simulation des Unterwasserlichts, charakterisiert
durch die ungeordnete Streuung durch die Wellen an der Oberfläche.
Eine einzelne Lichtquelle würde für diese Komposition unpassend
sein, weil sie den Schatten des Seeigels zu scharf wirken lassen würde.
Erzeugen durch externe Programme.
Ein Ray-tracer ist lediglich ein Werkzeug, eine komplette Szene mit Hilfe
einer formellen Ray-tracing Sprache zu erzeugen. Ray-tracer sind fähig,
Farb- und Lichtspezifikationen usw. zu erkennen. Manchmal braucht man Vorarbeit,
um die Entwicklungsarbeit zu unterstützen: 3D Scans, Formatumwandlunswerkzeuge,
und andere Programme. Trotzdem ist ein Ray-tracer nur eines in einer Reihe
von Werkzeugen für den Szenenaufbau und die Entwicklung. Mit anderen
Worten, Entwicklung durch das Eingeben der Ideen auf der Tastatur ist nicht
der einzige Mechanismus für die Herstellung künstlerischer Kompositionen,
wir haben Hilfswerkzeuge um komplexere Kompositionen herzustellen, die
nicht so einfach manuell in einer ray-tracer Sprache einzugeben sind. Als
Beispiel einer komplexen Szene, aufgebaut durch ein externes Programm,
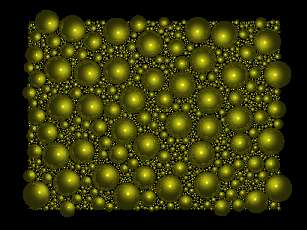
werden wir zunächst ein C-Programm namens burbujas.c (bubbles) verwenden.
Das Programm plaziert eine Anzahl von Blasen zufällig auf eine Oberfläche
der Größe 1000x750 pixels. Blasen können sich nicht untereinander
überschneiden, darum bestimmt unser Beispielcode zufällige Positionen
und Größen entsprechend. Wenn die neue Position ergibt, dass
eine Blase nahe neben eine existierende Blase fällt, wird eine neue
Position berechnet. Die Größe des Bereichs wird reduziert, um
sie passend zu machen. Nach einer großen Zahl von Wiederholungen
bekommt man eine Oberfläche mit fast keinem übrigen freien Raum.
Der Aufbau dieses detaillierten Beispiels fordert viel Rechenarbeit, weil
je mehr die Sequenz vorwärts kommt, es immer schwerer wird, eine neue
Blase zu plazieren.
burbujas.c
Nimm das Programm und lass es ablaufen. Adressiere den Standard-output
in einen Dateinamen 'burbujas.inc' um, damit die Daten für die Blasen
gespeichert werden (burbujas burbujas.inc). Die output-Datei beinhaltet
Werte wie diese:
sphere{<-375, 0, 33> 55.0000000 texture{Gold_Metal}} //(0/1)
sphere{< -86, 0, 62> 55.0000000 texture{Gold_Metal}} //(1/2)
sphere{<-326, 0, 346> 55.0000000 texture{Gold_Metal}} //(2/3)
sphere{< 190, 0, -156> 55.0000000 texture{Gold_Metal}} //(3/4)
sphere{< 62, 0, -293> 55.0000000 texture{Gold_Metal}} //(4/5)
sphere{< 323, 0, 161> 55.0000000 texture{Gold_Metal}} //(5/6)
sphere{< 341, 0, -15> 55.0000000 texture{Gold_Metal}} //(6/7)
...................
Ich empfehle etwas Geduld, weil es eine Weile dauert, eine output-Datei
zu generieren. An bestimmten Zeitpunkten kann man den Prozess unterbrechen
und die output-Datei bearbeiten, um sicherzugehen, dass die letzte Zeile
komplett ist. Wenn nicht, nimm sie einfach aus der Datei. Die Quelle für
pov folgen:
burbujas.pov
Der Quellcode beinhaltet wieder Hinweise auf das Symbol "clock", doch
diesmal hat es ein besonderen Grund. In diesem Fall generiert er nicht
eine Sequenz von Bildern für eine Animation, sondern vier Bilder mit
sehr unterschiedlichen Blickpunkten. Die Position, Winkel und Blende der
Kamera variiert unter den vier Bildern. Im vorherigen POVRAY-Artikel
erwähnten wir bereits, dass wir an einigen Punkten Beispiele untersuchen
werden , die die Möglichkeiten der Kamera in POVRAY erkunden. Gut,
das ist ein Beispiel. Es ist ganz einfach der Unterschied in dem fertiggerendertem
Bild entsprechend den Spezifikationen der Kamera. Man kann viele Perspektiven
erreichen entsprechend des Winkels der Blende: ein kleiner Winkel bringt
weite Perspektiven, während ein großer Winkel Nahaufnahmen erbringt.
Der Maximalwinkel ist 180 Grad, das ist ein sehr extremer Wert, denn es
ist schwer, Figuren zu unterscheiden. Die gezeigten Bilder sind auf
einem Pentium 200 MMX 48MB RAM (398 bogomips) bearbeitet worden. Es wurde,
wie angenommen, unter Nutzung des in den früheren Serien, 'pov', vorgesehenen
Werkzeuges ausgeführt:
pov burbujas 6 9 1 5 1 5
Total Time = Beschreiben der Parameterprüfung: Quellcode
ist burbujas.pov size 6 = (400x300) Quality 9 Intial
photogram = 1 Final photogram = 5 Initial clock = 1 Final
clock = 5 Die Zeit, die zum Generieren eines jeden Bildes benötigt
wird, ist wichtig. Mit höherer Qualität würde es folgende
Zeit in Anspruch nehmen: pov burbujas 9 9 1 5 1 5
Gesamtzeit = 4 1/2 Stunden .
Erstes Photogramm 2 Minuten
Zweites Photogramm 5 Minuten.
Drittes Photogramm 10 Minuten
Viertes Photogramm 13 Minuten
Fünftes Bild 4 Stunden !! Lasst uns nun die Resultate untersuchen.
Im ersten der vier Bilder ist die Kameraeinrichtung die einzige Änderung.
(Position, Winkel, Ausrichtung, usw.)


Befor das letzte Bild gezeigt wird, lasst mich ein anderes Thema durchgehen,
welches zur Würdigung dieses letzten Bildes relevant ist, das Thema
der CPU Optimierung.
CPU Anwendungsoptimierung
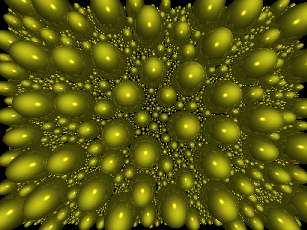
Das letzte Bild ist das komplexeste und POVRAY war nicht fähig, es
zu optimieren. Bei der Konfrontation mit komplizierten Kompositionen versucht
der ray-tracer, die Szene zu vereinfachen. In früheren Versionen von
POVRAY wurde die Optimierung von Hand getätigt; dazu hatte der Künstler
die Anweisung 'bounded_by' zur Spezifikation einer Primitive, die ein oder
mehrere Objekte einhüllen würde. Dann nahm der Ray-tracer an,
dass Strahlen, die nicht mit dieser Einhüllung kollidieren, auch nicht
mit einer der eingehüllten Objekte kollidieren würden. Das ist
eine Annäherung, die einige Rechenzeit spart. Es gibt sehr wenige
Fälle, bei denen das tatsächlich nützlich ist. Worauf es
hinausläuft, unser letztes Bild ist einer dieser Fälle!. Das
letzte Bild beinhaltet zu viele Objekte und ist sehr kompliziert. Deshalb
wäre es besser gewesen, die Komposition manuell zu optimieren, z.
B. durch Aufteilung der Blasen in Zonen, Verbinden von Blasen zu zusammengesetzten
Objekten, oder eben Verbinden all der Blasen in ein Objekt oder Einhüllen
der Gruppen von Kugeln mit dem gleichen Gebiet das Kommando 'bounde_by'
nutzend. Die Syntax würde sein:
union {
sphere { <x1, y1, z1>, r1 }
sphere { <x2, y2, z2>, r1 }
sphere { <x3, y3, z3>, r1 }
..........................
bounded_by { sphere { <xb, yb, zb>, rb } }
}
Die beschriebene Eingabe einer manuellen Optimierung kann bei Vereinigungen
und Schnittpunkten und auch bei jedem anderen Objekten genutzt werden.
Der Anwender kann andere Primitiven auswählen, wir wählen eine
Kugel, jedoch werden die besten Resultate oft mit Kästen und Kugeln
erreicht. Ist die Primitive ausgewählt, und bleibt ein Teil der zusammengestellten
Objektes draußen, kann das Ergebnis schadhaft sein. Ich möchte
nochmals betonen, dass man nur selten manuell optimieren muß. Unser
letztes Beispiel war eine Idee mit 'schlechter Absicht', mit einem voreilig
Befehl das Thema zu übersteigern. POVRAYs automatische Optimierung
war nicht fähig die Komposition zu vereinfachen. Es beinhaltet 2154
Kugeln. Der Leser könnte es nachprüfen, indem er sie zählt
:-).
In unserem Beispiel haben wir gezeigt wie man mit den Möglichkeiten
des Ray-tracers spielen kann. Oftmals kann die gleiche Idee oder das gleiche
Konzept auf verschiedenen Wegen ausgeführt werden, um verschiedene
Ergebnisse zu erhalten, und hier kann des Künstlers Kreativität
Ausdruck gewinnen.

Der Leser kann so einfache Bilder in vielen unterschiedlichen Szenarios
programmieren. POVRAY kann ein hilfreiches Werkzeug zum generieren synthetischer
Bilder sein, entweder statisch oder dynamisch.
Was wurde vergessen...?
Povray unterstützt viele mathematische Funktionen, manche mehr oder
weniger interessant. Leider wurde eine sehr interessante Funktion vergessen.
Es ist der "spline". Es ist nichts so bequem wie mit Stift und Papier ein
paar Punkte zu bestimmen und dann eine Funktion anzulegen, die eine
glatte Linie durch die Punkte zeichnet. POVRAY's spline Primitive kann
nicht als eine Funktion benutzt werden, statt dessen generiert es
eine Linie als die Grundlage zum Bau anderer Formen, es wäre besser,
wenn wir den spline für einige Variablen, die wir wünschen, anlegen
könnten. Das würde z. B. erlauben, dass die Kamera folgen kann
und die Flugbahn beliebig wird. Ich fände es ebenso großartig,
wenn einer externe Funktionen ausgeführt werden könnte. Zu einem
gewissen Grad kann all das durch Nutzung einbezogener und externer Programmierung
erreicht werden. Unter Linux haben wir eine Dienstleistung namens 'spline'.
Diese kann wie ein Kommando zum generieren der gewünschten Kurve aus
einem Satz von Punkten genutzt werden. Versuche, dieses Kommando mit externer
Programmierung zu kombinieren, z. B. Animationen oder Kamerabewegungen
zu berechnen.
Übungen
Optimierung des letzten Bildes dem bereits gegebenen Hinweis folgend.
Übersetze das Programm burbujas.c in die POVRAY Sprache. Übersetze
das Programm erizos.c in eine grundlegende zweckgebundene Sprache.
Leserbeiträge
Ich bin begierig, von Lesern zu hören und ihre Beiträge zu sehen,
vielleicht werden die rekursiven oder Schleifen-Strukturen hier diskutiert.
Bitte schickt mir eure Übungen als komprimierte Dateien. Es währe
großartig, Leserarbeiten
und und Arbeiten von Organisationen
zu einer Ausstellung im LinuxFocus Magazin zusammenzutragen. Ich werde
die interessantesten oder einfallsreichsten Bilder für die Ausstellung
aussuchen. Bitte keine kommerziell lizensierten Bilder einreichen.
Wenn möglich schickt auch die Quellcodes der Bilder, damit andere
Menschen aus euren Ideen lernen können.
pov3.tar.gz
(43 K bytes)[Alle Quellcodes für die Bilder in diesem Artikel]
2001-02-09, generated by lfparser version 2.9
![[Photo of theAuthor]](../../common/images/Antonio-C.gif)
![[Illustration]](../../common/images/illustration11.gif)
 sin(a) = A / C = (gegenüberliegende Seite / Hypothenuse)
sin(a) = A / C = (gegenüberliegende Seite / Hypothenuse) 




