![[LinuxFocus Image]](../../common/January1998/border-short.jpg)
| Duyumlar Belgelikler Kuruluşlar Öğütler |
OpenGL Programlama: Basit Çokgen GörüntüleştirimiYazar: Miguel Angel SepúlvedaÇeviri: Esma Meral |
Giriş
Noktaların Çizimi
Doğruların ve Çokgenlerin Çizimi
Alıştırmalar
Gelecek Yazı
GirişBu yazı, 2 ve 3 boyutlu grafikler için bir endüstri ölçünü (standardı) olan OpenGL hakkındaki makale dizisinin ilkidir. (Bakınız: OpenGL Nedir?). Okuyucunun, C geliştirme çalışmatabanına alışık ve GLUT kitaplığı hakkında bazı bilgilere sahip olduğunu kabul ediyoruz (Aksi durumda bu dergideki "GLUT programlama" konusundaki yazıların izlenmesi gerekir). Linux altında çalışırken, OpenGL konusunda özgür kullanıma açık eşsiz uygulamaları bulunan Mesa-kitaplığını kullanmanızı öneririz.Bu anda Mesa için donanım desteği bile bulunmaktadır. (Bakınız: 3Dfx grafik kartı). Yeni OpenGl güdümlerinin sunumu, en az bizim de yapmaya çabalayacağımız kadar, onun işlevselliğini kullanmaya çalışan bir örnek ile süregidecektir. Dizimizin sonunda bütünüyle OpenGL ile yazılmış bir oyun öykünümünü (simülasyonu), kaynak düzgüsüyle (koduyla) birlikte vereceğiz. Başlamadan önce, bir bilim adamı olduğum için, OpenGL deneyimimin büyük bir çoğunluğunun, OpenGL'in gerçel kuvantum ve kökleşik (klasik) sistemlerin öykünümlerini (simulasyonlarını) yazmak için bir araç olduğunu söylemek isterim. Bu nedenle örneklerim biraz bu yöndedir. ;-). Okuyucunun bu örnekleri erişilebilir ya da en azından eğlenceli bulacağını umuyorum. Eğer farklı örnekler görmek istiyorsanız, beni duyumlu kılmanız (haberdar etmeniz) yeterlidir. OpenGL, sıklıkla 3 boyutlu grafiklerle, özel etkilerle, karmaşık örneklerin ışıkla gerçek modellemesi gibi konularla ilgilidir. Bunun yanında 2 boyutlu grafikleri görüntüleştirmeye (render) yarayan bir makinedir. 3 boyutlu görüngelerin (perspektiflerin) karmaşıklığı, model görüntüleştirme, ışık, görüntüçeker (kamera) konumu ve bu gibi konuları öğrenmeye başlamadan önce 2 boyutta yapmayı öğrenebileceğiniz pek çok şey olması bakımından bu konu önemlidir. Mühendislikle ve bilimsel konularla ilgili çok sayıda uygulama 2 boyutta görüntüleştirilebilir (rendered). Dolayısıyla, ilk olarak bazı basit 2 boyut canlandırımlarının (animasyonlarının) nasıl yapıldığını öğrenmek yerinde olacaktır. Noktaların ÇizimiOpenGL yalnızca birkaç geometrik temelögeye sahiptir: noktalar, doğrular ve çokgenler. Bunların her biri kendilerine ait olan köşeler ile tanımlanır. Bir köşe 2 ya da 3 kayarnoktalı sayı (floating point number) ile özyapılandırılır (karakterize edilir), köşenin kartezyen koordinatları, 2 boyutta (x,y) ve 3 boyutta (x,y,z)'dir. Kartezyen koordinatlar çok yaygın olmakla beraber, bilgisayar grafiklerinde ayrıca her noktanın (x,y,z,w) 4 kayarnoktalı sayı ile gösterildiği benzeşik (homojen) koordinat sistemi de vardır. 3 boyutun temel özelliklerini inceledikten sonra bunlara geri döneceğiz. OpenGL'de tüm geometrik nesneler bir sıralı köşeler kümesi olarak tanımlandığından, bir köşenin belirtimi için bir yordam demeti bulunmaktadır.; Kullanımı şöyledir: void glVertex{234}{sifd}[v](TYPE coords); Haydi, bu kullanıma alışkanlık edinelim.{} imleri arasındaki sözcük yordamın adını göstermektedir.; Yordamlar short, long, float ya da double türde 2, 3 ya da 4 parametre alabilirler. Seçimebağlı olarak bu parametreler vektor formda verilebilir, biz v-tip yordamları kullanacağız. İşte bazı örnekler: void glVertex2s(1, 3);
float vector[3];
Basitleştirmek için bu yordamların tümü glVertex* olarak tanımlanırlar. OpenGL, herhangi bir köşe dizisini içeriğine göre yorumlar. Bu
içeriğin belirtimi glBegin(GLenum mode) ve
glEnd(), yordam ikilisiyle yapılmaktadır. Bu iki
yordam arasında çalıştırılan herhangi bir glVertex*
deyimi kip (mod) değerine göre yorumlanır. Örneğin: 2 boyutta 5 nokta çizer. GL_POINTS, OpenGL başlık dosyasında <GL/gl.h>. tanımlanmış etiketlerden birisidir. Daha pek çok uygun kip (mod) vardır ancak, bunlardan, gerektiğinde, sözedilecektir. Her nokta, OpenGL'in renk arabelleği (buffer) ile ilişkili durum
değişkenlerinde o anda saklanan renklerle çizilir. Geçerli
rengi değiştirmek için glColor* yordam demetini
kullanın. Renkleri seçmek ve uygulamak hakkında söylenecek çok şey
vardır (Diğer bir yazı yalnızca bu konuda olacaktır). 0.0'dan 1.0'a
kadar 3 tane kayarnoktalı değer kullanarak RGB (Kırmızı - Yeşil - Mavi)
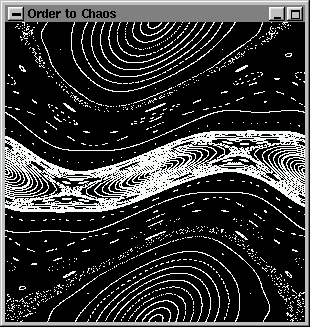
renkleri tanımlayabiliriz. Buraya kadar anlatılanlar ilk iki örnek düzgümüzü (kodumuzu) yazmak için yeterli malzemeyi oluşturmuş bulunmaktadır. İlk örnek, kargaşasal (kaotik) dönüşümde (ölçünlü dönüşüm, standart dönüşüm) birçok yörünge çizen basit bir OpenGL programıdır. Okuyucunun dönüşümler ve özellikle ölçünlü (standart) dönüşümler konusunda bilgili olmaması sorun değildir. Basitçe söylemek gerekirse, bir dönüşümün bir noktayı alıp iyi tanımlı bir bağıntı aracılığıyla yeni bir nokta üretir: yn+1 = yn + K sin(xn)
Ölçünlü (standart) dönüşüm durumunda yüklü bir parçacığın, parçacık hızlandırıcının simitinde hızlandırıcının düzlemini keserek yaptığı devinimde bıraktığı izi betimleyen bir model sözkonusu olur. Bunun ve diğer dönüşümlerin incelenmesi, çemberselhızlandırıcı içine kapatılmış bir yüklü parçacığın deviniminin kararlılığının anlaşılması açısında fizikte çok önemlidir. Ölçünlü (standart) dönüşüm, parametresinin bazı değerleri iğin K'nın açıkça kargaşasal (kaotik) ve tutuklu devinimin (trapped motion) bir karışımını göstermesinden dolayı çok donuktur??????. Sonuç olarak, fizik ile gerçekten ilgilenilmese de bir çok güzel grafik düzgü (kod) geliştirmek isteyenler ölçünlü (standart) dönüşümlere yeterince dikkat etmelidirler. Doku, ateş parlaması, ağaçlar, karaparçaları gibi şeyleri üretmekte kullanılan pek çok algoritma fractal dönüşümlere dayandırılmaktadır. ../../common/January1998/../../common/January1998/example1.c'nin kaynak düzgüsü (kodu):
#include <GL/glut.h>
#include <math.h>
const double pi2 = 6.28318530718;
void NonlinearMap(double *x, double *y){
static double K = 1.04295;
*y += K * sin(*x);
*x += *y;
*x = fmod(*x, pi2);
if (*x < 0.0) *x += pi2;
};
void winInit(){
/* Set system of coordinates */
gluOrtho2D(0.0, pi2, 0.0, pi2);
};
void display(void){
const int NumberSteps = 1000;
const int NumberOrbits = 100;
const double Delta_x = pi2/(NumberOrbits-1);
int step, orbit;
glColor3f(0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
y = 3.1415;
x = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
x = 3.1415;
y = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
};
int main(int argc, char **argv) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);
glutInitWindowPosition(5,5);
glutInitWindowSize(300,300);
glutCreateWindow("Standard Map");
winInit();
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Glut* yordamlarını anlamak için, GLUT Programlama
yazısını okuyabilirsiniz, Yukarıdaki düzgünün (kodun) çoğunluğu
oradan gelmektedir. Grafik penceresi tek arabellekte (buffer) ve RGB
kipte (modda) açılır. Bunun ardından display()
adlı geriçağırma fonksiyonu grafiği çizer: İlk olarak arkataban için kara
renk seçilir; glClear(GL_COLOR_BUFFER_BIT) renk arabelleğini geçerli renk
karaya yenidenkurar, daha sonra glColor ile beyaz renk seçildiktan sonra,
NonlinearMap() fonksiyonu birçok kez
çalıştırılır ve noktalar glVertex* fonksiyonu ile GL_POINTS kipte
(mod) çizdirilir. Yani gerçekten de kolay!
Pencere başlatım yordamında yani winInit()
'da OpenGL elaygıt takımından gelen yalnızca tek bir deyim
bulunduğuna dikkat çekmek gerekir:gluOrtho2D(). Bu yordam
2 boyutlu dik sistemin koordinatlarını gösterir. Fonksiyona geçen
parametreler "minimum x, maksimum x, minimum y, maksimum y" dir. ../../common/January1998/example1'i çalıştırdıktan sonra şu şekli göreceksiniz:
Şimdi ikinci programa geçelim, ../../common/January1998/../../common/January1998/example2.c:
Dikkate değer diğer bir farklılık ise display() fonksiyonunun
sonunda glutSwapBuffers() fonksiyonunun kullanılmasıdır. Pencere
ikili arabellek kipinde açılmıştır, dolayısıyla tüm görüntüleştirme
yönergeleri gizliarabelleğe uygulanır; bu durumda kullanıcı şeklin çizimini
görememektedir. Şeklin çizimi tamamen bittikten sonra glutSwapBuffers()
ile gizli ve görünür arabelleklerin görevleri değiştirilir Bu teknik
olmaksızın animasyon düzgün bir şekilde çalışmaz.
Canlandırım (animasyon) süresince görüntülenen bazı şekiller:
ÖNEMLİ: display() geriçağırma fonksiyonu , idle() fonksiyonundan önce
en az bir kere yaşamageçirilir. Canlandırımlarınızı (animasyonlarınızı)
yazarken ve display() ile idle() fonksiyonlarına hangi değerlerin
geçtiğine karar verirken bunu aklınızdan çıkarmayın.
Önceden sözedildiği üuzere glBegin(GLenum mode)
çeşitli kipler (modlar) köşe dizilerini alabilir. Ardarda belirtimi
yapılan v0, v1,v2,v3,
v4,..., vn-1 uygun biçimde yorumlanabilir.
Olası kip (mod) değerleri ve gerçekleştirilen eylemler aşağıda
belirtilmiştir:
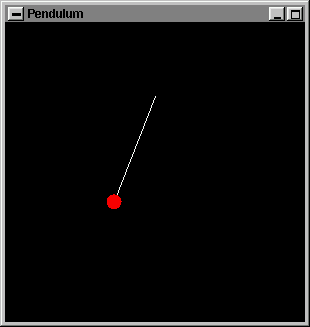
Üçüncü örneğimizde GL_LINES ve GL_POLYGON'nun kullanımını gösteren
başka bir canlandırım (animasyon) vardır. Programı derleyin, kaynak
düzgüsüne (koduna) bakın ve nasıl çalıştığını inceleyin. Example2.c'ye
oldukça benzerdir, burada çok basit bir sarkacın devinimi (hareketi)
çizdirilmiştir. Canlandırım ülküsel (ideal) bir sarkacın devinimini
öykünmektedir (simüle etmektedir). İşte canlandırımdan bir
anlıkgörüntü (snapshot):
Önceden olduğu gibi yine idle() adlı, amacı saati çalışır
tutmak olan yani time değişkenini güncelleyen, bir geriçağırma
fonksiyonu bulunmaktadır. display() , iki nesne çizer;
sarkacın ipi ve ağırlığı (sırasıyla beyaz ve kırmızı renklerde).
Sarkaç koordinatlarınin devinimi xcenter ve ycenter için verilen
bağıntılardan kapalı olarak elde edilebilmektedir::
Öğrendiklerinizi uygulamak için bazı öneriler:
Şu anda söyleyeceklerim bu kadar. Çokgenler hakkında daha tartışılacak
çok şey var. Bir sonraki sayıda (Mart 1998) çokgenleri araştırmaya devam
edeceğiz ve zaten kullanmaya alışık olduğunuz bazı güdümlerin ayrıntılarına
inip modellemesini yapacağız..
|
- Donanım Taraması: 3Dfx Grafik Kartı adlı yazıyı okuyabilir,
- http://www.opengl.org/'a danışabilir ve
- Yazarın diğer yazılarını okuyabilirsiniz: OpenGL Nedir?, GLUT Programlama: Pencereler ve Canlandırımlar.
Bu sanalyörenin bakımı Miguel A Sepulveda tarafından yapılmaktadır.