Introductie in cryptografie

ArticleCategory:

System Administration

AuthorImage:

TranslationInfo:[Author and translation history]

original in fr Pierre Loidreau

fr to en Axelle Apvrille

en to nl Hendrik-Jan Heins

AboutTheAuthor

Pierre werkt als docent/onderzoeker aan de ENSTA (Ecole Nationale Supérieure de Techniques Avancées). Zijn onderzoeksveld omvat "cryptosystemen" gebaseerd op de theorie van foutcorrectie codes. hij "speelt" dagelijks met Linux... en tennist vrij veel.

Abstract:

Dit artikel is eerder gepubliceerd in een speciale editie van Linux Magazine France over beveiliging. De editor, de auteurs en de vertalers waren zo vriendelijk om LinuxFocus ieder artikel van deze speciale editie te laten publiceren. LinuxFocus zal deze zodra ze naar het Engels vertaald zijn ter beschikking stellen. Dank aan alle mensen die zich bezig houden met dit werk. Deze samenvatting zal worden gebruikt voor alle artikelen met dezelfde oorsprong.

ArticleIllustration:

ArticleBody:[The article body]

Waarom cryptografie - 2500 jaar geschiedenis.

De oorsprong van cryptografie gaat waarschijnlijk terug tot de begintijd van de menselijke beschaving, vanaf het moment dat mensen leerden te communiceren. Ze moesten contunu zoeken naar middelen om er zeker van te zijn dat gecommuniceerde geheimen ook geheim bleven. Het eerste opzettelijke gebruik van technische middelen om berichten te coderen, is terug te vinden bij de Grieken. Rond 6 jaar voor Christus werd er bij hen een stok genaamd de "scytale" gebruikt. Degene die het bericht stuurde, bond een stuk papier om de stok en schreef er in de lengterichting een bericht op. Daarna haalde hij het papier van de stok en stuurde het naar de bedoelde ontvanger. Het decoderen van het bericht zonder kennis van de dikte van de stok -die hier de sleutel is- zou vrijwel onmogelijk moeten zijn. Later maakten de Romeinse legers gebruik van Caesar's code om te communiceren (een drie posities alfabet-verplaatsing, dus voor een "a" een "d" en voor een "d" een "g").

In de volgende 19 eeuwen zijn er meer en minder geavanceerde experimentele coderings-technieken verzonnen, waarbij de veiligheid afhing van hoeveel vertrouwen de gebruiker er in had. In de 19e eeuw schreef Kerchoffs over de principes van de moderne cryptografie. Een van die principes zegt dat de veiligheid van een cryptografisch systeem niet afhangt van het gebruikte cryptografische proces, maar van de gebruikte sleutel.

Dit zijn dus belangrijke randvoorwaarden die worden gesteld aan cryptografische systemen. De bestaande systemen misten echter nog steeds een mathematische achtergrond, en dus ook de greeedschappen om te meten hoe gevoelig ze waren voor aanvallen en kraak-pogingen. Het zou nog mooier zijn als iemand een 100% veilig systeem zou kunnen maken, het absolute einddoel! In 1948 en 1949 werd er een wetenschappenlijke achtergrond opgesteld door Cluade Shannon, hij schreef twee essay's over het onderwerp: "A Mathematical Theory of Communication" en, nog belanrijker "The Communication Theory of Secrecy Systems". Deze artikelen maakte een einde aan hoop en vooroordelen. Shannon bewees dat Vernam's codering - ook bekend als het "One Time Pad" -, die slechts een paar jaar eerder was voorgesteld, de enige onvoorwaardelijk veilige methode was die oit zou kunnen worden ontwikkeld. Helaas echter is dit systeem in de praktijk onwerkbaar... Dit is de reden waarom evaluatie van de huidige systemen gebaseerd is op te berekenen veiligheid. Een geheime versleutelmethode is pas veilig als geen enkele bekende berekenmethode beter en sneller werkt dan een oneidig aantal pogingen tot de correcte sleutel gevonden is.

AES (Advanced Encryption Standard)

In oktober 2000 heeft het Amerikaanse NIST (National Institute of Standards and Technology) de goedkeuring van een nieuwe geheime versleutelcode aangekondigd, die is gekozen uit 15 kandidaten. Dit nieuwe standaard algoritme is bedoeld als vervanging van het oude DES algoritme waarvan de sleutellengte te klein begon te worden. Rijndael - een samengetrokken naam van de uitvinders, Rijmen en Daemen- werd uitgekozen als de toekomstige AES.

Dit encryptiesysteem is een zogenaamde "block" cipher, dit houdt in dat berichten worden gecodeerd met behulp van 128-bit blokken. Er bestaan meerdere mogelijkheden voor de blokgrootte, zoals 128, 192 of 256 bit sleutels. Ter informatie: DES codeert 64 bit blokken met een sleutel van slechts 56 bit. Triple DES codeert normaal gesproken 64 bit blokken met een 112-bit sleutel.

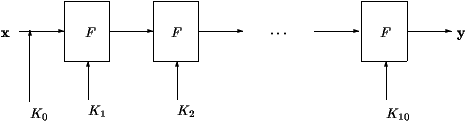
Tabel 1: AES iteraties
De werking van AES is beschreven in figuur 1. Allereerst wordt het bericht bitsgewijs, dus bit per bit, gewijzigd volgens een logische XOR bewerking met de sleutel. Daarna wordt, zoals bij alle block-coderingen, de fucntie F steeds herhaald, waarbij subsleutels worden gebruikt die berekend worden uit de eerste sleutel d.m.v. een expansie routine.

Voor AES wordt de functie F 10 maal geïtereerd.

Figuur 2 beschrijft hoe functie F wordt geïtereerd voor de codering. Een 128-bit blok dat 16 bytes bevat, wordt als invoer gebruikt. Eerst wordt er een permutatie S toegepast op iedere byte. Daarna wordt er een tweede permutatie P toegepast op de 16 bytes. De 128-bit subsleutel die gegenereerd is door de sleutel expansie routine wordt nu bits-gewijs toegevoegd aan het voorgaande resultaat.
Sleutel Ki van ongeveer n°i wordt verkregen uit de sleutel expansies routine met behulp van de subsleutel K(i-1) van ongeveer n°i-1 en K0 de geheume sleutel. De sleutel expansie routine is beschreven in fuguur 3. De 16 bytes van sleutel K(i-1) worden 4 aan 4 verwerkt.
De laatste 4 bytes worden gepermuteerd met behulp van permutatie S - dezelfde permutatie die wordt gebruikt in de iteratiefunctie F om de bits van iedere byte te permuteren. Daarna worden de eerste 4 resulterende bytes toegevoegd aan een 'alpha' element. Dit element is een voorgedefinieerde byte die afhankelijk is van een geheel getal. Tenslotte worden de 4 resulterende bytes bitsgewijs toegevoegd aan de eerste 4 bytes van K(i-1), om Ki te verkrijgen. Daarna wordt het resultaat toegevoegd aan de volgende 4 bytes, enzoverder.

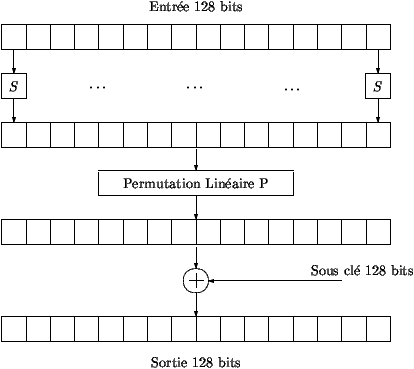
Tabel 2: Functie F
Laten we nu eens in het kort kijken naar hoe substituties worden opgebouwd, en welke constante aⁱ deze voor bedoeld is. Technisch gezien - en voor de eenvoudigheid - moet een byte worden gezien als een element uit een set van 256 elementen (een eindig veld genaamd) en daarop worden allerlei eenvoudige operaties (zoals additie, vermenigvuldiging en hun inversen) losgelaten.
In feite is de substitutie S, zoals eerder genoemd een inverse in zo'n veld. Substitutie P is aangegeven als een zeer eenvoudige operatie en kan daarom ook eenvoudig worden geïmplementeerd. Element aⁱ correspondeert met een machtsverheffing i met een element uit het veld. Zulke overwegingen maken de implementaties van AES zeer efficiënt.

AES bestaat uit slechts twee zeer eenvoudige bytegewijze operaties, wat AES twee grote voordelen oplevert:

zelfs pure software implementaties van AES zijn zeer snel. Bijvoorbeeld een C++ implementatie op een Pentium 200Mhz geeft een 70Mbits/s prestatie bij het versleutelen ;
de weerstand van AES tegen differentiale en lineaire crypto-analyse is niet afhankelijk van de keuze van de S-Box, zoals bij DES waar de S-Boxes ervan verdacht werden dat ze een achterdeur bevatten voor de NSA. Eigenlijk zijn alle operaties eenvoudig.

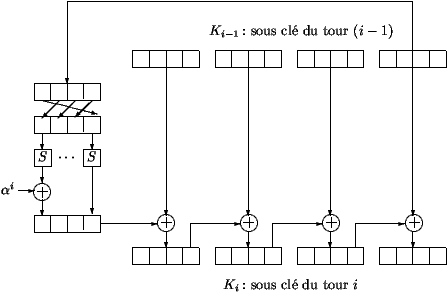
Tabel 3: Sleutel expansie routine

Publieke sleutel cryptografie

In 1976 publiceerden Diffie en Hellman een artikel ganaamd "New Directions in Cryptography", dit was een echt nieuwtje in de cryptografiegemeenschap. Dit artikel introduceert het concept van de publieke sleutel cryptografie. In feite was de enige familie van toen bekende algoritmen - symmetrische sleutel algoritmen - niet meer voldoende, er waren nieuwe toepassingsgebieden ontstaan door de explosieve groei in communicatiemethoden, zoals netwerken, waardoor deze algoritmes niet langer voldeden.

In feite was de kern van het nieuwe idee het concept van een eenrichtings-valdeur (trapdoor) functie. Zulke functies zijn eenvoudig in één richting te bedienen, maar zijn onmogelijk te inverteren zonder kenis te hebben van de valdeur - ook al is de functie zelf algemeen bekend. Nu dient de publieke sleutel als functie, terwijl de valdeur (alleen bekend bij een beperkt aantal gebruikers) een private sleutel genoemd wordt. Dit leidde tot de geboorte van Alice en Bob (en anderen). Alice en Bob zijn twe personen die proberen te communiceren en hun gesprek intact trachten te houden, ze willen geen inmenging van derden die proberen af te luisteren of de communicatie willen vervalsen.

Om het bericht te ontcijferen, hoeft de ontvanger alleen maar de functie te inverteren, met behulp van het valluik natuurlijk.

Het beste voorbeeld van een publieke sleutel cryptosysteem (en zeker de eenvoudigste) is twee jaar later, in 1978 gepresenteerd. Deze is uitgevonden door Rivest, Shamir en Adleman - afgekort dus RSA. Het is gebaseerd op het mathematische probleem van het tot een macht verheffen van gehele getallen. De private sleutel is opgebouwd uit een driedeel (p,q,d) met p en q als twee priemgetallen (van ongeveer dezelfde grootte), en d een relatief priemgetal met p-1 en q-1. De publieke sleutel bestaat uit een paar (n,e), met n=pq, en e het inverse van d modulus (p-1)(q-1), dus

ed = 1 mod(p-1)(q-1).

Stel dat Alice een tekst wil sturen naar Bob, gecodeerd met Bob's publieke sleutel (n,e). Ze transformeert de boodschap eerst in een geheel getal m kleiner dan n. Daarna doet ze het volgende

c = m^e mod n,

en stuurt het resultaat c door naar Bob. Aan zijn kant verwerkt Bob, wiens publieke sleutel (p,q,d) is:

c^d mod n = m^ed mod n = m.

Voor RSA is de valdeur functie de functie die een geheel getal x <n tot waarde x^e mod n verandert.

Sinds RSA zijn er veel andere cryptosystemen met een publieke sleutel uitgevonden. Een van de bekendste hedendaagse alternatieven voor RSA is gebaseerd op discrete logaritmes.

Hedendaags gebruik van cryptografie

De publieke sleutel cryptografie is zeer interessant, omdat het eenvoudig te gebruiken is en het vele veiligheidsproblemen oplost die voorheen onopgelost waren gebleven. Het is meer bepaald een oplossing voor enkele authenticatie problemen:

Individuen Identificeren: omdat ze gebruik maakt van de hedendaagse communicatiesystemen, is annonimiteit geen probleem, maar Alice wil wel zeker weten dat degene met wie ze praat de echte Bob is, en niet iemand die zich voordoet als Bob. Om hier zeker van te zijn maakt ze gebruik van een identificatieprotocol. Er bestaan meerdere communicatie protocollen, ze vertrouwen meestal op de principes van RSA of op discrete logaritmes.
Document authenticatie: een autoriteit authenticeert documenten met behulp van een digitale handtekening. De handtekening bestaat uit enkele bits die het resultaat zijn van enkele bewerkingen met als input het document en de autoriteit, dezen worden meestal "verhashed" met behulp van een "hash" algoritme zoals MD5 of SHA. Iedereen die toegang heeft tot het document zou moeten kunnen verifiëren dat deze handtekening daadwerkelijk afkomstig is van de autoriteit. Om dit mogelijk te maken, wordt er gebruik gemaakt van handtekening schema's. Eén van de bekendste schema's is ElGamal - dat ook is gebaseerd op discrete logaritmische problemen.

Net als de systemen met geheime sleutels kan publieke sleutel cryptografie de vertrouwelijkheid van een communicatie waarborgen.

Laten we er vanuitgaan dat Alice in het geheim wil communiceren met Bob. Alice haalt Bob's publieke sleutel op uit een publieke directory, en codeert haar bericht met deze sleutel. Zodra Bob deze gecodeerde tekst ontvangt, gebruikt hij zijn private sleutel om de gecodeerde tekst te ontcijferen, en leest hij het geschrevene. De beide sleutels spelen een zeer verschillende rol, daarom heet dit soort cryptografie ook asymmetrische versleuteling - cryptografie met dezelfde geheime sleutel voor het versleutelen en het decoderen staat bekend als symmetrische versleuteling.

Publieke sleutel cryptografie biedt nog een voordeel boven geheime sleutel cryptografie. Als n gebruikers communiceren met behulp van een geheime sleutel cryptografie systeem, heeft ieder van hen een andere geheime sleutel voor ieder ander in de groep nodig. Dus er moeten n(n-1) sleutels beheerd worden. Als n groter is dan enkele duizenden gebruikers, dan moeten er dus al miljoenen sleutels worden beheerd... Bovendien is het toevoegen van een nieuwe gebruiker aan de groep geen eenvoudige opgave, aangezien er n nieuwe sleutels moeten worden gemaakt zodat de gebruiker kan communiceren met de anderen in de groep. En daarna moeten al die sleutels ook nog eens worden verzonden aan alle leden van de groep. Bij asymmetrische cryptosystemen zijn alle n publieke sleutels van de leden opgeslagen in een publieke directory. Het toevoegen van en nieuwe gebruiker bestaat alleen maar uit het toevoegen van zijn publieke sleutel aan deze directory.

Het gebruik van een publieke of een geheime sleutel: het evenwicht zoeken

De voorgaande paragraaf heeft uitgelegd dat publieke sleutel cryptografie vele problemen heeft opgelost waarvoor private sleutel cryptografie niet toereikend was. Je kunt je afvragen waar AES eigenlijk voor is ontwikkeld. Er zijn echter twee belangrijke verklaringen voor deze keuze.

Allereerst een praktische reden: Over het algemeen is publieke sleutel cryptografie zeer traag. Software implementaties van RSA zijn bijvoorbeeld duizenden malen trager dan AES en RSA is niet ontwikkeld met het oog op hardware implementatie. Het verzenden van gegevens is op dit moment zo'n cruciaal gegeven dat we een limitatie van een versleutelingsalgoritme simpelweg niet kunnen accepteren.
Ten tweede leidt de interne structuur van publieke sleutel cryptosystemen tot andere beveiligingsproblemen.

Publieke sleutel cryptosystemen hebben bijvoorbeeld een veel grotere sleutel nodig dan geheime sleutel cryptosystemen om hetzelfde beveiligingsniveau te halen. Het verband tussen sleutellengte en veiligheid is eigenlijk alleen van toepassing op de symmetrische versleuteling. Dit soort systemen vertrouwt namelijk op het feit dat ze alleen gebroken kunnen worden door een "brute-force" aanval, dit betekent dus dat alle mogelijke sleutels geprobeerd worden. Als de sleutelgrootte 128 bits is, dan moeten er dus 2¹²⁸ mogelijke sleutels geprobeerd worden.

Bij de asymmetrische versleuteling is de sleutellengte alleen een interessant gegeven als hetzelfde systeem wordt bekeken, RSA met een 512 bit sleutel is bijvoorbeeld minder veilig dan AES met een 128 bit sleutel. De enige manier om een publieke sleutel cryptosysteem op de juiste manier te beoordelen is het inschatten van de complexiteit van de best bekende aanval, en dit is iets heel anders: je weet nooit of een nieuwe vinding de beveiliging van een systeem kan compromitteren. Kort geleden heeft een groep wetenschappers met succes een 512 bit geheel getal gefactorreerd. Dus, voor een goede beveiliging wordt op dit moment een 1024 bit sleutel geadviseerd.

Dit betekent dus dat voor pure versleutelingstoepassingen de voorkeur uitgaat naar geheime sleutel algoritmen -als het mogelijk is om deze te gebruiken. Zimmermann heeft aan een interessante hybride opsossing gewerkt, deze is geïmplementeerd in PGP. Als Allice en Bob met elkaar willen communiceren met behulp van een symmetrisch algoritme (PGP maakt gebruik van IDEA), verloopt de communicatie als volgt:

Alice en Bob onderhandelen over een geheime sleutel met behulp van een sleutel uitwisselingsprotocol. Sleutel uitwissel protocollen maken gebruik van publieke sleutel cryptografie. Een van de bekendste protocollen berust op het algoritme van Diffie-Hellman.
Daarna communiceren ze verder met behulp van het symmetrische IDEA algoritme.

Zodra ze uitgecommuniceerd zijn, wordt de onderhandelde 'sessiesleutel' weggegooid. Zo'n systeem maakt gebruik van zowel een geheime sleutel als een publieke sleutel. Meestal wordt het sleutel uitwissel protocol gezien als het minst veilige deel van het systeem

Bibliografie

Geschiedenis van cryptografie:

S. Singh : Histoire des codes secrets. Jean-Claude Lattès, 1999.
D. Kahn : The Codebreakers: the story of secret writing. MacMillan publishing, 1996.

Over AES:

Cryptografie in het algemeen:

Een Artikel van Anne Canteaut en Fran Lévy-dit-Véhel : http://www-rocq.inria.fr/canteaut/crypto_moderne.pdf
B. Schneier : Applied Cryptography. John Wiley en Sons, 1996.