![[Photo of the Author]](../../common/images2/RalfWieland2.jpg)
original in de Ralf Wieland
de to en Jürgen Pohl
en to it Davide Lo Vetere
Mi occupo di ambienti di simulazione, reti neurali e sistemi fuzzy. Questi ultimi sono stati sviluppati su Linux (a partire da 0.99pl12). Mi interesso anche di elettronica e di hardware e del porting di soluzioni su Linux.
![[Illustration]](../../common/images2/article345/symbol.png)
Lavoro in un istituto di ricerca
che si occupa di ricerca sui paesaggi.
Affrontiamo problemi come questi:
La preparazione del lavoro come l'analisi dei dati, la loro scrematura, la formattazione di dati diversi, la presentazione per l'elaborazione etc., sono tutte operazioni che possono essere eseguite egregiamente con Linux. Anche se si pensa che i vari Excel di turno possano fare tutto, la combinazione di Perl, Emacs, octave [www.octave.org], R [www.r-project.org] etc. si rivela essere una validissima alternativa nella battaglia coi dati. Perl è molto versatile e il suo impiego non si limita alla conversione dei dati; può interrogare database (MySQL), eseguire calcoli, etc., è molto performante, riutilizzabile, portabile. In particolare la riutilizzabilità del codice è importante in quanto il lavoro manuale porta con sé errori nei dati e questa fonte di errore si elimina facilmente utilizzando codice ben collaudato. Scrivere articoli con LaTeX convince immediatamente attraverso la qualità tipografica del testo. Linux fornisce strumenti che lo rendono estremamente attraente per l'ambito di lavoro scientifico. Non vogliamo nascondere uno svantaggio: si deve avere una certa pratica nell'utilizzare questi strumenti. Non tutto si può fare in modo intuitivo e non tutti sono degli "smanettoni".
Perché mai uno dovrebbe sviluppare strumenti da sé? Non
c'è gia tutto disponibile?
Ci sono software per la simulazione estremamente performanti, uno
per tutti Matlab
[www.mathworks.com]. Per processare dati geografici sono disponibili i
Geographic Information Systems (GIS) come ARCGIS
[www.esri.com/software/arcgis] o l'equivalente free Grass [grass.itc.it].
Per le statistiche vale lo stesso discorso. Dunque perché sviluppare?
La questione non è la performance del singolo stadio di calcolo
ma la interconnessione dei diversi componenti all'interno del sistema globale.
In una simulazione le varie attività computazionali sono eseguite da diversi
programmi, che potrebbero comunicare tra loro in modo inefficiente, magari attraverso
interfacce create dall'utente. Ad accentuare questo aspetto c'è il fatto che i dati
sono in quantità massicce (dati spaziali) e con alti margini d'errore.
Il cuore del sistema di simulazione deve contemplare questo aspetto. In altri termini
un algoritmo deve fornire dati utili all'intera simulazione anche quando
è alimentato da dati non perfettamente coerenti, nel qual caso dovrebbe anche
segnalare il fatto.
L'elaborazione di quantità massicce di dati (matrici con più di un milione di
elementi sono la norma) richiede algoritmi altamente efficienti.
Algoritmi robusti e performanti possono spesso essere sviluppati da sé.
Lo svantaggio dei sistemi commerciali risiede nella segretezza dei sorgenti.
Come possono gli scienziati sviluppare e far circolare modelli se i
sorgenti non sono accessibili?
Da queste considerazioni si è deciso di sviluppare lo "Spatial Analysis and Modeling Tool"
(SAMT) come strumento open source.
E' uno strumento di simulazione che offre la possibilità di
manipolare dati, di interfacciarsi con MySQL e con GIS. Contiene
le funzioni fondamentali per trattare i dati di origine raster,
per manipolare dei raster (blending, distanze, interpolazioni, etc.)
e può generare presentazioni bi- e tri-dimensionali dei dati.
Nota: i dati di tipo raster si ottengono dividendo una mappa
attraverso una griglia a trama fine. L'informazione è archiviata
in strati di dati cosiddetti raster appunto.
Un modello accede all'informazione così strutturata in strati.
Oltre all'accesso verticale delle informazioni, ha grande rilevanza
l'informazione in prossimità di ciascun livello cui si accede.
Quest'ultima infatti è la base per il modellamento dei fenomeni connessi
SAMT genera il riferimento nel quale gli strumenti - come il
(velocissimo) interprete fuzzy e il neural network tool
(nnqt) - possono essere impiegati. I modelli fuzzy
servono a integrare delle informazioni specifiche nella
simulazione.
Un esperto può spesso descrivere e persino controllare un processo
anche se non ha di esso un modello matematico.
In sostanza le Reti Neurali sono processi che ci permettono di
derivare delle relazioni funzionali fra delle misure.
Quanto segue introduce allo sviluppo delle strumento per lo studio
delle reti neurali.
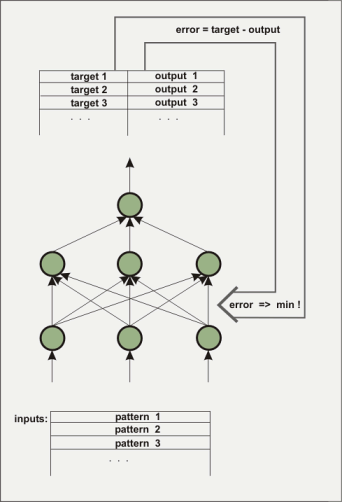
Una Rete Neurale artificiale consiste di diversi strati. Il primo strato è alimentato dai dati iniziali coi quali si addestra la rete, questi dati sono in forma di numeri floating-point. Lo strato intermedio, tra lo strato di ingresso, ossia quello dei dati, e quello d'uscita, non è direttamente visibile: esso è detto 'hidden layer' (strato nascosto). Spesso sono diversi gli strati nascosti. Lo strato d'uscita dell'esempio è costituito solo di un elemento. Questo tipo di architettura è usato per costruire una funzione a partire da diversi input e un solo output. Gli strati nascosti sono necessari per ricostruire mappe non-lineari, per esempio la funzione x^2-y^2. Come fa una rete a conoscere la funzione attesa? Inizialmente, è ovvio, la rete non conosce la funzione. Le connessioni tra i vari nodi della rete, ovvero l'assegnazione di pesi ai vari elementi, è operata attraverso un procedimento stocastico di assegnazione dei valori. Durante l'apprendimento l'algoritmo prova a cambiare i pesi dei nodi in modo che l'errore quadratico medio tra un output predeterminato e quello così calcolato sia minimo. Esiste una gamma di algoritmi per ottenere questa minimizzazione dell'errore quadratico medio e non la descriveremo qui. In nnqt sono implementati tre algoritmi. Il sistema progredisce condizionatamente agli ingressi per un designato output, questo processo è anche detto di 'supervised learning' (apprendimento condizionato).

La rete è istruita per evidenziare se ha raggiunto un livello d'errore
accettabile a partire dai dati d'ingresso e dai dati di controllo (è
utile suddividere parte dei dati prima della fase di apprendimento
per utilizzarli in seguito come dati di controllo per verificare
sia la performance del sistema sia l'effettivo apprendimento).
L'attribuzione dei pesi ai nodi determina il comportamento della rete.
Cosa si può effetivamente fare con una rete? Oltre all'utilizzo di
questo strumento in ambito scientifico, c'è una serie di altre applicazioni
più o meno convenzionali. Ci sono degli impieghi delle reti neurali per
predire quali saranno le tendenze dei mercati finanaziari. Non ho avuto
successo in questo ma magari qualcun'altro ce la farà.
Un'altra possibilità interessante potrebbe essere l'uso delle reti neurali
per le previsioni meteorologiche a breve termine. I dati delle stazioni
di rilevazione meteo, per esempio, potrebbero essere utilizzati per
istruire una rete neurale. Utili sarebbero dati come la pressione atmosferica
e i suoi cambiamenti, così come i dati sulle precipitazioni.
Di fatto le variabili usate nelle stazioni di rilevamento sono questi.
Un rete neurale lo potrebbe fare meglio? Per supportare la sperimentazione
in ogni direzione nnqt è GPL.
Gli scienziati cominciarono lo sviluppo del neural network tool con la richiesta che si potessero analizzare i dati raccolti. Volevano uno strumento il più semplice possibile, che potesse essere utilizzato per applicazioni spaziali, vale a dire: volevano poter mettere in relazione i risultati con dei riferimenti spaziali. Naturalmente, ci sono degli eccellenti strumenti per lo studio delle reti neurali sul mercato. Sono disponibili persino strumenti free come SNNS [www-ra.informatik.uni-tuebingen.de/SNNS/] o librerie come fann [fann.sourceforge.net]. SNNS è ottimo, ma non è facile da usare per chi non sa programmare perché fornisce un output in codice C. Il risultato che offre è al di sopra delle esigenze di un utente non esperto. nnqt doveva rispondere a dei requisiti specifici:
Lo sviluppo ha avuto luogo nei seguenti passi:
C'è una straordinaria quantità di eccellente letteratura
sulle reti neurali. Un testo particolarmente rappresentativo
è questo.
Tuttavia, si incontra a volte una certa distanza che si colma con la
propria esperienza e condividendo l'esperienza altrui. Ho apprezzato
l'agile lavoro con Matlab che utilizza l'applicazione dell'algoritmo di
Levenberg-Marquardt.
Solo dopo una estesa ricerca in internet ho trovato un
articolo [www.eng.auburn.edu/~wilambm/pap/2001/FastConv_IJCNN01.PDF][copia locale,
105533 bytes] che descrive l'uso di questo algoritmo nelle reti neurali.
Questa è la base. Ho dovuto "solo" integrare la tanh (tangente iperbolica)
nell'algoritmo, perché la preferisco. Anche per questo ho utilizzato Linux,
un software per l'algebra al calcolatore: Maxima [maxima.sourceforge.net].
Con questo sistema è possibile manipolare complesse equazioni,
applicare ad esse operatori differenziali e così via, insomma
operazioni che non sono sempre semplici da risolvere con carta e penna.
Maxima ha reso possibile eseguire le opportune manipolazioni algebriche
e implementare la prima versione dell'algoritmo C in nel lavoro di un week-end.
L'implementazine C è stata fatta per test e per affinare i parametri.
Utilizzando il sistema di simulazione open source desire [members.aol.com/gatmkorn]
(i miei ringraziamenti al suo creatore, il Prof. Korn!) come strumento comparativo,
ho potuto eseguire i primi calcoli sul modello.
Il nuovo algoritmo così implementato non era malaccio. Il tempo ad istruire
la rete per il problema xor, un test principe per le reti neurali, ha richiesto
in media 70ms su un Pentium 3GHz. (Molto di questo tempo è usato
nelle operazioni di lettura dall'hard disk, il tempo nei vecchi Athlon 750MHz era infatti
appena più alto).
Come alternativa, il ben noto algoritmo di "back propagation" è stato
implementato e analizzato. Dopo questa preparazione, che è la base per futuri
miglioramenti degli algoritmi, l'implementazione dello strumento è proseguita
Come ambiente di sviluppo prediligo qt, è ben documentato e posso usare Emacs. Il qt designer ti assiste nel disegno della GUI. Nonostante ciò queste opzioni non sono sufficienti nello sviluppo di nnqt. Ho avuto bisogno di oggetti come diagrammi, cursori etc. In questo la comunità di sviluppatori si è rivelata, ancora una volta, utile. Le librerie di qwt [qwt.sourceforge.net] e qwt3d [qwtplot3d.sourceforge.net] possono essere utilizzate per abbreviare drasticamente il tempo di sviluppo. Con questi sorgenti, nnqt è stato costruito in due settimane. Quando ero soddisfatto del risultato l'ho girato agli utenti. Avevano un sacco di richieste! L'insieme di dati doveva essere diviso automaticamente negli insiemi di addestramento della rete e di test, volevano poter assegnare dei nomi per migliorare l'organizzazione del lavoro, più analisi - come grafici con curve parametriche, etc. Insomma alcune cose ho potuto integrarle facilmente e in poco tempo, per altre ci vorrà più tempo. Ecco alcuni screenshots:
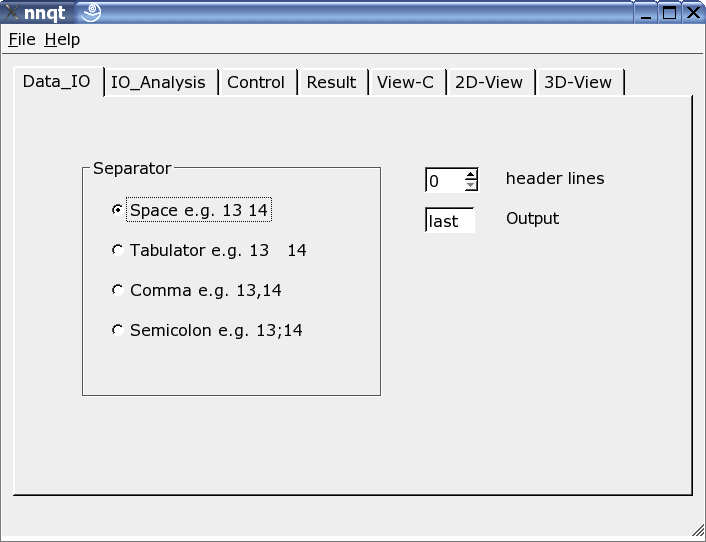
Qui il reader può essere adattato ai dati in ingresso. Vari separatori sono consentiti, si possono nascondere delle linee di intestazione e si può scegliere il target dei dati. Nota: il formato di dati deve essere noto, dato che nnqt dipende da questi.
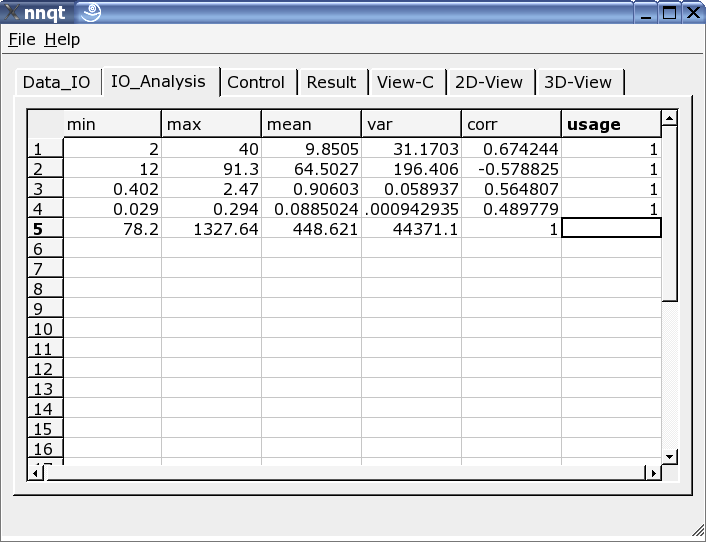
Dopo aver fornito correttamente i dati al sistema possiamo andare alla pagina di analisi. Qui troviamo alcune informazioni sui dati e dobbiamo selezionare i dati per l'apprendimento da tutte le colonne. Un '1' nell'ultima colonna indica che il valore è selezionato per l'apprendimento. (Si possono utilizzare fino a 29 valori per l'apprendimento.)
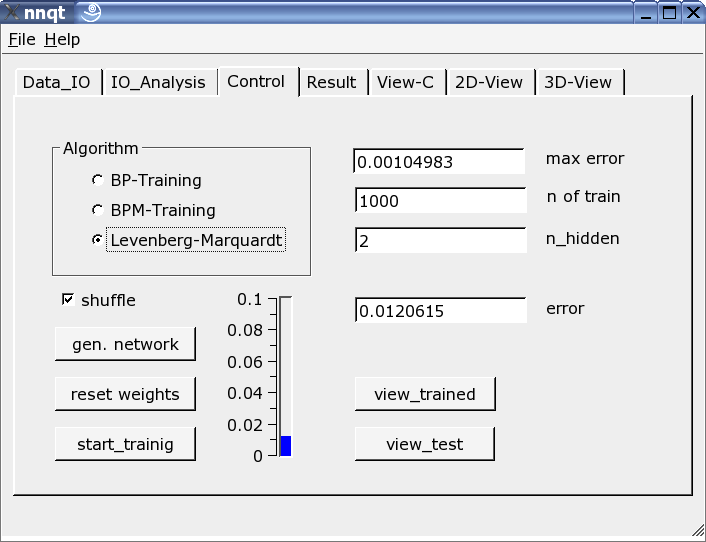
Molto importante è la pagina di controllo. Il numero di elementi nascosti, il numero di passi di apprendimento e l'algoritmo con cui la rete apprende sono definiti qui. L'apprendimento può essere tracciato sul riferimento verticale con una barra e con un valore. Questo deve essere ripetuto finché il parametro iniziale è stocasticamente valutato e il valore ottenuto in uscita è una funzione di questo parametro. Selezionando l'opzione "shuffle" si genera una selezione casuale - anziché sequenziale - dei dati di apprendimento. Qualche volta questo approccio si rivela utile. Se siamo riusciti a ridurre l'errore quadratico medio a valori utili alla simulazione, possiamo ottenere i primo grafico premendo il bottone "view_trained":
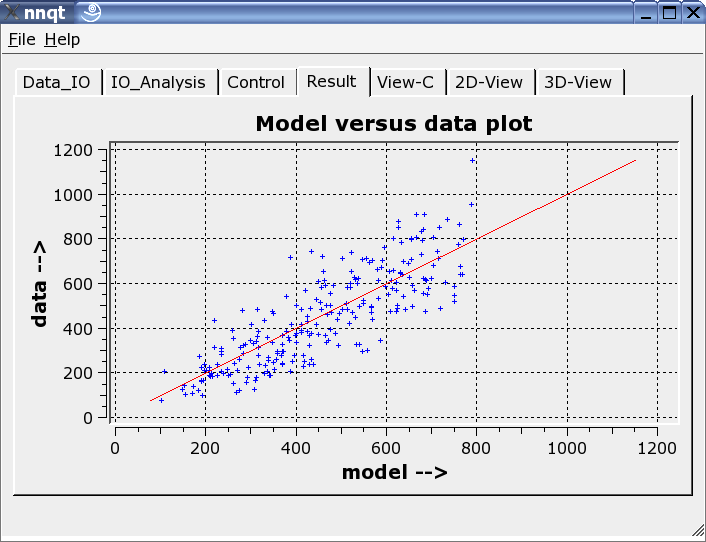
Questo mostra il raffronto dei dati di apprendimento con i dati generati direttamente dalla rete neurale. Teoricamente i dati dovrebbero posizionarsi lungo la diagonale. Ma questa situazione è ideale e non può essere completamente soddisfatta! Tuttavia, i risultati nel complesso sono accettabili. (I dati di controllo - ovvero i dati per i quali non c'è stato apprendimento - sono mostrati in rosso.) Il passo successivo permette lo studio dello sviluppo della funzione. I valori di riferimento devono essere significativi per il sistema. E questo è un aspetto importante, dal momento che il comportamento della rete rimane attendibile per valori di ingresso prossimi ai valori con cui la rete è stata precedentemente istruita.
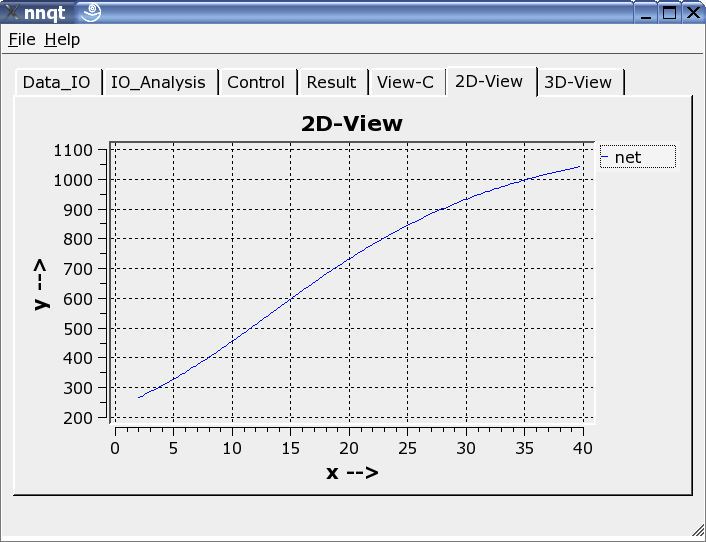
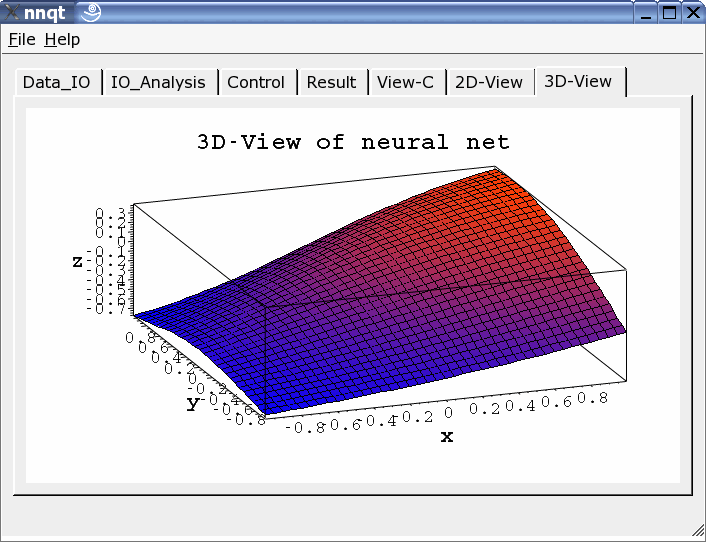
Si possono scegliere rappresentazioni bi- e tri-dimensionali.
nnqt è codice open source, è stato rilasciato sotto GPL.
Chiunque può usarlo liberamente e migliorarlo. E quest'ultima
possibilità è particolarmente caldeggiata.
L'installazione è semplice. Devono essere installate solo le librerie
qwt e qt.
nnqt.tgz è semplice da scompattare (tar-zxvf nnqt.tgz). Questo
creerà una nuova directory di nome nnqt. Passando a cd nnqt,
e poi a qmake e a make si completa l'installazione.
Se tutto si è svolto correttamente bisogna fornire alla shell questa variabile con:
export NN_HOME=/path_a_nnqt
Se nnqt viene aperto in un'altra shell, i dati e i modelli
dovrebbero essere visti da nnqt. Spero che vi ci possiate divertire.
Per testare il programma è stato incluso un insieme di dati e due input.
Qualcuno riconosce qual'è la funzione appresa dalla rete?
(è x^2-y^2 nell'intervallo [-2..2].)
Cosa potremmo creare con questo - Sono curioso di conoscere le vostre idee.
Abbiamo dimostrato che Linux è un eccellente ambiente di sviluppo per risolvere problemi scientifici. Ho potuto sviluppare questo software grazie a codice preesistente di ottima qualità, senza il quale, sarebbe stato impossibile creare uno strumento operativo nel breve tempo di 6 settimane. E' sempre bello poter usare software libero. Per questo, i miei ringraziamenti vanno ai molti sviluppatori il cui lavoro rende possibile tutto quello che facciamo su Linux.
James A. Freeman:
"Simulating Neural Networks with Mathematica", Addison-Wesley
1994