![[LinuxFocus Image]](../../common/January1998/border-short.jpg)
| Nouvelles Archives |
Programmation OpenGL : Rendu de Polygones Simplespar Miguel Angel Sepúlveda |
Introduction
Dessiner des Points
Dessiner des Lignes et des Polygones
Exercises
La prochaine fois...
IntroductionCeci est le premier article de la série consacrée à OpenGL, un standard de l'industrie en matière d'infographie 2 et 3D (voir Qu'est ce qu' OpenGL). Nous considererons que le lecteur connait son propre environnement de developpement en C et possède quelques connaissance de la bibliothèque GLUT (sinon, suivez les articles consacrés à "la programmation GLUT" dans cette revue. Avec Linux, nous recommandons l'utilisation de la bibliothèque Mesa qui est une superbe implantation gratuite d'Open-GL. Il existe meme maintenant un support materiel pour Mesa (voir Les cartes Graphiques 3Dfx ). Chaque présentation d'une nouvelle commande OpenGL sera accompagnée d'exemples qui essaieront (au moins !) d'exploiter ses fonctionnalités. A la fin de cette série d'articles, nous présenteront le code source d'une simulation de jeux completement écrite avec OpenGL. Avant de commencer, je voudrais attirer l'attention sur le fait que comme je suis un scientifique, mon expérience avec OpenGL se résume principalement à écrire des simulations de quantas réels et de systèmes classiques. Aussi, mes exemples sont orientés ;-). J'espère que les lecteurs trouveront ces exemples accessibles ou du moins amusants. Si vous etes intéressés par d'autres exemples, n'hésitez pas à me le faire savoir. OpenGL est souvent associé avec le graphisme 3D, des beaux effets spéciaux, des modèles complexes avec des modèles d'éclairages réalistes etc... Toutefois, c'est aussi une machine de tracé garphique 2D. Ce point est important car on peut apprendre beaucoup de choses avec deux dimensions avant d'entrer dans la complexité des perspectives 3D, le modelage, l'éclairage, le positionnement des caméras etc ... Un grand nombre d'applications industrielles et scientifiques, utilise les tracés 2D. Commençons donc par voir comment vréer de simple animation dans un plan. Dessiner des PointsOpenGL n'a que quelques primitives géométriques : points, lignes, polygones. Tous sont décrits par des vecteurs. Un vecteur est caractérisé par 2 ou 3 points réels, les coordonnées Cartésiennes du vecteur, (x,y) en 2D et (x,y,z) en 3D. Bien que les coordonnées Cartésiennes soient les plus courantes en infographie , il existe aussi le système homogène de coordonnées dans lequel chaque point est décrit par 4 nombres réels (x,y,z,w). Nous y reviendrons après avoir introduit des notions de tracés en 3D. Puisqu'avec OpenGL, tous les objets géométriques sont décrit en termes de vecteurs ordonnés, il y a une fammille de fonctions pour déclarer un vecteur. Sa syntaxe est : void glVertex{234}{sifd}[v](TYPE coords); La notation devra vous devenir familière. Les accolades indiques une partie du nom de la fonction. Cette dernière peut prendre 2,3 ou 4 parametres soit de type entiers, entiers longs, réels ou doubles. Ces parametres peuvent etre fournit optionnellement sous forme de vecteurs, auquel cas, le nom de la fonction comportera un v. Voici quelques exemples : void glVertex2s(1, 3);
float vector[3];
A titre de simplification, toutes ces fonctions sont appellées glVertex*. OpenGL interprètes une séquence quelconque de vecteurs
selon son contexte. Le contexte est déclaré par la paire
de fonctions glBegin(GLenum mode) et glEnd().
Toute instruction glVertex* executée entre
les deux est interprétée en fonction de la valeur de mode,
par exemple:
dessine 5 points en 2D avec les coordonnées spécifiées. GL_POINTS est une des constantes définies dans le fichier d'entete <GL/gl.h>. Il existe de nombreux autres modes disponibles mais nous les décrirons au fur et à mesure des besoins. Chaque point est tracé avec la couleur mémorisée
par la variable d'état OpenGL associée au tampon des couleurs.
Pour changer de couleur, on utilise la famille de fonctions glColor*;
il y a beaucoup à dire sur la sékection et la manipulation
des couleurs (ceci fera l'objet d'un article séparé). Pour
l'instant, nous utiliserons 3 nombres réels variants de 0.0 à
1.0. C'est le codage RVB (Rouge-Vert-Bleu):
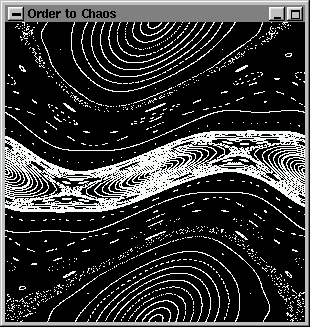
Nous en savons déjà assezpour écrire deux premiers exemples de code. Le premier est un programme OPenGL simple qui trace un nombre donné d'orbites dans une projection chaotique (La projection standard). Cela n'a pas d'importance si vous n'etes pas habitués aux projections et à la projection standard en particulier. En termes simples, une projection, prend un point et en génère un autre à partir d'une formule précise: yn+1 = yn + K sin(xn)
Dans le cas de la projection standard, il représente la trace
que laisse une particule chargée qui décrit des cercles autour
d'un tore d'un accélérateur de particules et en traverse
une section plane. L'étude de ces propriétés et d'autres
projections est importante en physique car elle nous aide à comprendre
la stabilité de la particule chargée confinée dans
le cyclotron.
#include <GL/glut.h>
#include <math.h>
const double pi2 = 6.28318530718;
void NonlinearMap(double *x, double *y){
static double K = 1.04295;
*y += K * sin(*x);
*x += *y;
*x = fmod(*x, pi2);
if (*x < 0.0) *x += pi2;
};
void winInit(){
/* Set system of coordinates */
gluOrtho2D(0.0, pi2, 0.0, pi2);
};
void display(void){
const int NumberSteps = 1000;
const int NumberOrbits = 100;
const double Delta_x = pi2/(NumberOrbits-1);
int step, orbit;
glColor3f(0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
y = 3.1415;
x = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
x = 3.1415;
y = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
};
int main(int argc, char **argv) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);
glutInitWindowPosition(5,5);
glutInitWindowSize(300,300);
glutCreateWindow("Standard Map");
winInit();
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Lisez s'il vous plait, l'article Programmation
de GLUT pour comprendre les fonction glut*. La majorité de ceprogramme
viens de là. La fenetre graphique est ouverte en mode tampon simple
et RGB. Une fonction de rappel nommée display()
trace la projection: d'abord nous sélectionnons la couleur noire
pour le fond; glClear(GL_COLOR_BUFFER_BIT) initialise le tampon de couleurs
à la couleur courante (noir), puis après avoir choisi la
couleur blanche avec glColor, nous lançons la fonction NonlinearMap()
plusieurs fois et traçons les points avec glVertex* en mode
GL_POINTS. Vraiment simple.
Remarquer que dans la fonction d'initialisation winInit()
il n'y a qu'une seule instruction du la bibliothèque d'utilitaires
OpenGL, gluOrtho2D().
L'exécution de l'exemple 1 donne l'image suivante :
Passons maintenant au second programme, ../../common/January1998/../../common/January1998/example2.c:
Une autre différence remarquable est l'utilisation de glutSwapBuffers()
à la fin de display(). La fenetre a été
initialisée en mode double-tampon, en conséquence, toutes
les instruction de tracés sont appliquées au tampon caché;
l'utilisateur ne peut pas voir l'image se dessinner dans ce cas. Une fois
que l'image complète est terminée, elle est rendue visible
en inversant les tampons avec glutSwapBuffers(). Sans cette technique,
l'animation n'est pas fluide.
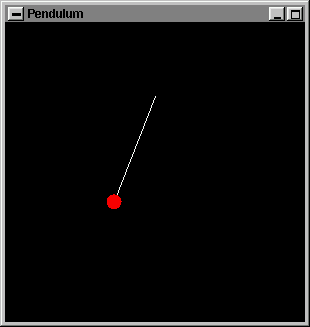
Voici quelques images dessinnées pendant l'animation :
IMPORTANT: La fonction de rappel display() est
toujours appelée au moins une fois, avant idle(). N'oubliez pas
ceci en écrivant vos animamtions et au moment de répartir
ce qui va dans display() et idle().
Nous avons déjà mentionné que glBegin(GLenum
mode) accepte divers modes et que les séquences de vecteurs
v0, v1,v2, v3,v4,...
vn-1 déclarés à postérioi sont interprétés
en conséquence. Les valeurs possibles du mode et les actions associées
sont :
Comme précedemment, il ya une fonction de rappel idle()
dont le but est de maintenir l'orloge animée (en mettant à
jour la variable time). display() trace deux objets;
la corde et le poids du pendule (en white et red respectivement). Le mouvement
des coordonnées du pendule est implicite dans les formules de xcenter
et ycenter:
Voici des suggestions pour pratiquer ce que vous avez déjà
appris :
C'est tout pour aujourd'hui. Il reste encore beaucoup de choses à
dire sur les polygones. Dans le prochain numéro, (March 1998)
nous continuerons à explorer les polygones et nous traiteront en
détail certaines des commandes que vous connaissez déjà.
|
Traduit par John Perr
- Lisez Le matériel:Les cartes Graphiques 3Dfx.
- Consultez http://www.opengl.org/.
- Lisez d'autres articles du même auteur:Qu'est ce qu'OpenGL?, Programmation GLUT: Fenêtres et Animations.
Ce site Web est maintenu par Miguel A Sepulveda.