HomeMapIndexSearchNewsarchivesLinksabout LF
[Top Bar]
[Bottom Bar]
[Photo of the Author]
Miguel Angel Sepulveda

M@ail an den Autor

Inhalt
Einleitung
Punkte zeichnen
Zeichnen von Linien und Polygonen
Aufgaben
Ausblick
Literaturverweise

OpenGL Programmierung,Teil I: Rendern von einfachen Polygonen


Zusammenfassung:
Mit diesem Artikel startet die Serie über den Einsatz von OpenGL, einer Bibliothek für die Programmierung von 2D und 3D Grafiken.


Einleitung

Dies ist der erste Artikel einer Serie über OpenGL, einen Industriestandard für 2D/3D Grafik (siehe Artikel Was ist OpenGL). Der Leser sollte mit der ihm zu Verfügung stehenden C Entwicklungsplattform vertraut sein. Außerdem sollte er ein wenig mit der GLUT Bibliothek umgehen können, ansonsten wird ihm die Artikelserie "GLUT Programmierung" im LinuxFocus ans Herz gelegt. Unter Linux wird der Einsatz der Mesa Bibliothek, die eine erstklassige freie Implementierung von OpenGL ist, vorgeschlagen. Für diese existiert nun sogar Hardwareunterstützung (siehe Artikel 3Dfx Grafikkarte).

Jedesmal, wenn OpenGL Befehle vorgestellt werden, wird dies anhand von Beispielen geschehen, in denen versucht wird, deren Funktionalität voll auszuschöpfen. Am Ende der Serie wird der Quelltext einer Spielesimulation, die komplett unter Nutzung von OpenGL geschrieben wurde, präsentiert.

Bevor es hier losgeht, sollte erwähnt werden, daß ich Wissenschaftler bin und ich meine Erfahrungen mit OpenGL als Werkzeug für die Programmierung von Simulationen von klassischen und Quantensystemen gemacht habe. Deswegen könnten die Beispiele ein wenig unkonventionell sein ;-). Ich hoffe, der Leser wird die Beispiele verständlich oder zumindest amüsant finden. Sollte jemand andere Arten von Beispiele sehen wollen, so gilt: einfach melden.

OpenGL wird oft mit 3D Grafik, tollen Spezialeffekten, komplexe Modellen mit realistischen Lichteffekten, usw. in Verbindung gebracht. Jedoch ist es auch eine 2D Rendermaschine. Dies ist recht wichtig, da Vieles im Bereich der 2D Grafikprogrammierung gelernt werden kann, bevor man sich mit den komplexen Sachverhalten der 3D Grafiken, wie Perspektiven, Modellberechnungen, Lichtquellen, Kamerapositionierung usw. beschäftigen will. Eine große Zahl von technischen und wissenschaftlichen Anwendungen arbeiten im 2D Grafikbereich. Deswegen werden zuerst einfache 2D Animationen betrachtet.

Punkte zeichnen

OpenGL stellt nur ein paar wenige geometrische Primitive bereit: Punkte, Linien und Polygone. Alle diese Objekte werden über ihre Eckpunkte beschrieben. Ein Punkt wird über 2 oder 3 Fließkommazahlen charakterisiert, Karthesischen Koordinaten des Punktes (x,y) im 2D bzw. (x,y,z) im 3D Bereich. Während das karthesische Koordinatensystem allgemein verbreitet ist, so ist im Bereich der Computergrafik auch das inhomogene Koordinatensystem in Gebrauch. In diesem System wird jeder Punkt durch 4 Fließkommazahlen (x,y,z,w) bestimmt. Dieses wird später nochmals betrachtet, nachdem einige grundlegende Dinge im Bereich 3D Grafik vorgestellt worden sind.

Da in OpenGL alle geometrischen Objekte schließlich als eine geordnete Menge von Eckpunkten beschrieben werden, steht ein ganzer Satz von Funktionen für die Deklaration eines Punktes zur Verfügung. Dabei sieht die Syntax wie folgt aus:

void glVertex{234}{sifd}[v](TYPE coords); 

Der Leser sollte sich mit dieser Schreibweise vertraut machen. Die geschweiften Klammern umfassen einen Teil des Namens der Funktion. Die Funktionen können 2, 3 oder 4 Parameter erwarten, die vom Typ short, long, float oder double sind. Alternativ können diese Parameter auch in Vektorform übergeben werden. In diesem Fall würden die v-Typ Funktionen benutzt werden. Hier sind einige Beispiele:

void glVertex2s(1, 3);
void glVertex2i(23L, 43L);
void glVertex3f(1.0F, 1.0F, 5.87220972F);

float vector[3];
void glVertex3fv(vector);

Diese Funktionen werden im folgenden einfach als glVertex* bezeichnet.

OpenGL interpretiert eine Folge von Punkten immer im aktuellen Kontext. Der Kontext wird durch das Funtionenpaar glBegin(GLenum mode) / glEnd() begrenzt, alle glVertex* Anweisungen dazwischen werden entsprechend dem Wert von mode interpretiert, zum Beispiel:
glBegin(GL_POINTS);
glVertex2f(0.0, 0.0);
glVertex2f(1.0, 0.0);
glVertex2f(0.0, 1.0);
glVertex2f(1.0, 1.0);
glVertex2f(0.5, 0.5);
glEnd();

Dadurch werden 5 Punkte im 2 dimensionalen Bereich entsprechend den Koordinaten spezifiziert. GL_POINTS ist einer der in der OpenGL Headerdatei <GL/gl.h> definierten Bezeichner. Es gibt noch viele andere Modi, diese werden bei Bedarf näher betrachtet.

Jeder Punkt wird in der aktuellen Farbe gezeichnet, die in der entsprechenden OpenGL Zustandsvariable gespeichert ist, welche mit dem Farbpuffer assoziiert ist. Die aktuelle Farbe wird über die Familie der glColor* Funktionen geändert. Das Thema der Auswahl und Manipulation von Farben ist recht ausgedehnt (dieses wird in einem eigenen Artikel behandelt werden). Im Moment wird mit 3 Fließkommazahlen zwischen 0.0 und 1.0 gearbeitet - mit der RGB (Rot-Grün-Blau) Farbkodierung;
glColor3f(1.0, 1.0, 1.0); /* White */ 
glColor3f(1.0, 0.0, 0.0); /* Red */ 
glColor3f(1.0, 1.0, 0.0); /* Magenta */ 
etc... 

Download: ../../common/January1998/Makefile, ../../common/January1998/../../common/January1998/example1.c, ../../common/January1998/../../common/January1998/example2.c

Dies ist schon genug Material, um unsere ersten beiden Beispiele zu schreiben. Das erste Beispiel ist ein einfaches OpenGL Programm, das eine Reihe von Kreise in eine chaotische Abbildung (Standard-Abbildung) schreibt. Wenn der Leser nicht mit Abbildungen - insbesondere der Standard-Abbildung - umgehen kann, ist das nicht schlimm. Einfach gesagt handelt es sich um rekursive Zuordungen, bei denen der nächste Punkt aus dem vorigen Punkt berechnet wird.

yn+1 = yn + K sin(xn)
xn+1 = xn + yn+1

In diesem Fall der Standard Abbildung wird z.B. die Spur eines geladenen Teilchens in einem Teilchenbeschleuniger beschrieben. Die Koordinaten geben an, an welchen Stellen das Teilchen die Schnittebenen des Beschleunigertoruses durchquert. Die Untersuchungen dieser und anderer chaotischen Abbildungen sind in der Physik wichtig, um die Stabilität von Trajektorien (in diesem Fall der Teilchenbahn im Zyklotron) zu verstehen. Die Standard Abbildung ist deshalb besonders interessant, weil für bestimmte Werte von K deutlich sowohl choatisches als auch nicht-chaotisches Verhalten beobachtet wird. Auch wenn man nicht wirklich an der Physik interessiert ist, sollte man diesen Abbildungen und ihren Eigenschaften etwas Aufmerksamkeit schenken, da sich schöne, fraktale Bilder erzeugen lassen. Mit fraktalen Algorithmen, die auf chaotischen Abbildungen basieren, lassen sich z.B. Strukturen, Flammenbilder , Bäume, Landschaften und andere Texturen erzeugen.

Hier nun der Quelltext von ../../common/January1998/../../common/January1998/example1.c: 

#include <GL/glut.h>
#include <math.h>  

const  double pi2 = 6.28318530718;

void NonlinearMap(double *x, double *y){
    static double K = 1.04295;
    *y += K * sin(*x);
    *x += *y;
    *x = fmod(*x, pi2);
    if (*x < 0.0) *x += pi2;
};

void winInit(){
    /* Set system of coordinates */
    gluOrtho2D(0.0, pi2, 0.0, pi2);
};

void display(void){
    const int    NumberSteps = 1000;
    const int    NumberOrbits = 100;
    const double Delta_x = pi2/(NumberOrbits-1);
    int step, orbit;

    glColor3f(0.0, 0.0, 0.0);
    glClear(GL_COLOR_BUFFER_BIT);
    glColor3f(1.0, 1.0, 1.0);

    for (orbit = 0; orbit < NumberOrbits; orbit++){
      double x, y;
      y = 3.1415;
      x = Delta_x * orbit;

      glBegin(GL_POINTS);
      for (step = 0; step < NumberSteps; step++){
        NonlinearMap(&x, &y);
        glVertex2f(x, y);
      };
    
      glEnd();
    };

    for (orbit = 0; orbit < NumberOrbits; orbit++){
      double x, y;
      x = 3.1415;
        y = Delta_x * orbit;

        glBegin(GL_POINTS);
        for (step = 0; step < NumberSteps; step++){
          NonlinearMap(&x, &y);
          glVertex2f(x, y);
        };
        glEnd();

     };
};

int main(int argc, char **argv) {
  glutInit(&argc, argv);  
  glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);  
  glutInitWindowPosition(5,5);  
  glutInitWindowSize(300,300);  
  glutCreateWindow("Standard Map");  
  
  winInit();
  glutDisplayFunc(display);  
  glutMainLoop();  
  
  return 0;  
}  

Der Leser sollte sich den Artikel zur Programmierung von GLUT durchlesen, damit er den Einsatz der glut* Funktionen versteht, ein Großteil des Codes wurde von dort übernommen. Das Grafikfenster wird in den Modi Single Buffer und RGB geöffnet. Eine Callback Funktion namens display() zeichnet das Bild: Zuerst wird Schwarz für den Hintergrund ausgewählt; glClear(GL_COLOR_BUFFER_BIT) setzt den Farbpuffer auf die aktuelle Farbe (Schwarz) zurück; nachdem dann Weiß mittels glColor selektiert wurde, wird NonlinearMap() mehrere Male ausgeführt und die Punkte mittels glVertex* im GL_POINTS Modus gezeichnet, wirklich einfach.

Man beachte, daß in der Initialisierungsroutine winInit() des Fensters eine Anweisung der OpenGL Hilfsbibliothek benutzt wird, gluOrtho2D(). Durch diese Funktion wird ein 2D orthogonales Koordinatensystem erzeugt. Die übergebenen Parameter sind "minimales X, maximales X, minimales Y, maximales Y".
Es wurde ein Fenster im Single Mode gewählt mit einer großen Zahl von Punkten, sodaß man den Bildaufbau mitverfolgen kann. Für Single Mode Fenster ist es typisch, daß bei großen und rechenintensiven Bildern Objekte auf dem Schirm dargestellt werden, sobald die entsprechenden OpenGL Routinen aufgerufen werden.

Nach Start von ../../common/January1998/example1 sollte folgendes Bild zu sehen sein:

 

Nun wird das zweite Programm, ../../common/January1998/../../common/January1998/example2.c, betrachtet: 
 
#include <GL/glut.h> 
#include <math.h>

const  double  pi2 = 6.28318530718; 
const  double  K_max = 3.5;
const  double  K_min = 0.1;
static double  Delta_K = 0.01;
static double  K = 0.1;          


void NonlinearMap(double *x, double *y){
    /* Standard Map */
    *y += K * sin(*x);
    *x += *y;

    /* Angle x is module 2Pi */
    *x = fmod(*x, pi2);
    if (*x < 0.0) *x += pi2;
};


/* Callback function: 
   What to do in absence of use input */
void  idle(void){
    /* Increase the stochastic parameter */
    K += Delta_K;
    if(K > K_max) K = K_min;

    /* Redraw the display */
    glutPostRedisplay();
};


/* Initialization for the graphics window */
void winInit(void){
    gluOrtho2D(0.0, pi2, 0.0, pi2);
};

/* Callback function:
    What to do when the display needs redrawing */
void display(void){
    const int    NumberSteps = 1000;
    const int    NumberOrbits = 50;
    const double Delta_x = pi2/(NumberOrbits-1);
    int step, orbit;

    glColor3f(0.0, 0.0, 0.0);
    glClear(GL_COLOR_BUFFER_BIT);
    glColor3f(1.0, 1.0, 1.0);
                
    for (orbit = 0; orbit < NumberOrbits; orbit++){
        double x, y;
        y = 3.1415;
        x = Delta_x * orbit;

        glBegin(GL_POINTS);
        for (step = 0; step < NumberSteps; step++){
          NonlinearMap(&x, &y);
          glVertex2f(x, y);
        };
        glEnd();
     };

     for (orbit = 0; orbit < NumberOrbits; orbit++){
        double x, y;
        x = 3.1415;
        y = Delta_x * orbit;

        glBegin(GL_POINTS);
        for (step = 0; step < NumberSteps; step++){
          NonlinearMap(&x, &y);
          glVertex2f(x, y);
        };
        glEnd();
     };

     glutSwapBuffers();
};


int main(int argc, char **argv)  {  
  /* GLUT Initializations */
  glutInit(&argc, argv);  
  glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA);  
  glutInitWindowPosition(5,5);  
  glutInitWindowSize(300,300);
  
  /* Open Window */
  glutCreateWindow("Order to Chaos");  
  
  /* Window initializations */
  winInit();

  /* Register callback functions */
  glutDisplayFunc(display);  
  glutIdleFunc(idle);

  /* Launch event processing */
  glutMainLoop();  
  
  return 0;  
}  
  
    

Das Programm basiert auf ../../common/January1998/../../common/January1998/example1.c. Hauptunterschied ist, daß das Fenster im Double Buffer Modus geöffnet wird, und der Parameter K der Berechnungen eine Variable ist, deren Wert sich während des Programmablaufes ändert. Eine neue Callback Funktion, idle(), wird mittels glutIdleFunc() bei der Ereignisverwaltung von GLUT angemeldet. Diese Funktion hat eine besondere Bedeutung, sie wird jedes Mal aufgerufen, wenn kein Ereignis durch Eingabe des Benutzers registriert wurde. Die Funktion idle() ist ideal für die Programmierung von Animationen. In ../../common/January1998/example2 wird sie für die Variation des Parameters K verwendet. Am Ende der Funktion findet man eine andere nützliche GLUT Anweisung, glutPostResDisplay(), welche den Fensterinhalt neu darstellt, wobei die alten Eistellungen beibehalten werden. Im allgemeinen ist es effektiver, diese Funktion, statt erneut display(), zu verwenden.

Ein anderer erwähnenswerter Unterschied ist der Einsatz von glutSwapBuffers() am Ende von display(). Das Fenster wurde im Double Buffer Modus initialisiert. Alle Berechnungen werden auf dem nicht sichtbaren Puffer durchgeführt. Dem Benutzer bleibt der Bildaufbau in diesem Fall verborgen, erst nachdem das ganze Bild (Frame) vollständig berechnet worden ist, wird es durch den Wechsel von sichtbaren und versteckten Puffer mittels glutSwapBuffers() dargestellt. Ohne diese Technik würden Animationen nicht weich ablaufen.

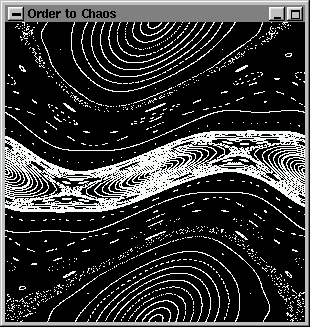
Hier sind einige Bilder zu sehen, die während der Animation dargestellt werden.:

 

WICHTIG: Die display() Callback Funktion wird immer mindestens einmal vor idle() durchlaufen. Dies sollte nicht vergessen werden, wenn man eine Animation programmiert und entscheidet, was in display() und was in idle() geschehen soll.

Zeichnen von Linien und Polygonen

Download:
../../common/January1998/../../common/January1998/example3.c

Wie vorher schon erwähnt, können durch glBegin(GLenum mode) verschiedene Modi ausgewählt werden, in denen jeweils die nachfolgende Deklaration von Punkten v0, v1,v2, v3,v4,... vn-1 entsprechend interpretiert wird. Mögliche Werte für den Modus und die jeweilige Interpretation der Punkte sieht wie folgt aus:

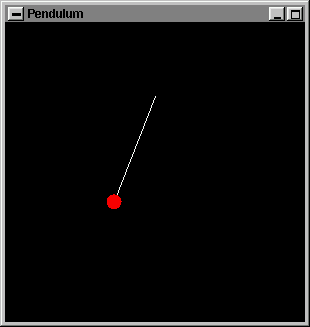
Im dritten Beispiel, eine weitere Animation, werden GL_LINES und GL_POLYGON verwendet. Nach dem Kompilieren und dem Testlauf sollte der Leser einen Blick auf den Quelltext des Programmes werfen und die Funktionsweise studieren. Prinzipiell ähnelt es ../../common/January1998/../../common/January1998/example2.c. Das Bild, was nun gezeichnet wird, ist ein einfaches Pendel, wobei die Bewegung eines idealen Pendels simuliert wird. Hier ist ein Schnappschuß der Animation:
 

Wie zuvor auch, gibt es hier eine idle() Callback Funktion, deren Aufgabe es ist, die Uhr laufen zu lassen (Die Variable time wird aktualisiert). Die Funktion display() zeichnet zwei Objekte: Die Schnur des Pendels und das Gewicht (jeweils in Weiß und in Rot). Die Wanderung der Koordinaten des Pendels steckt implizit in den Formeln für xcenter und ycenter: 

      
void display(void){
  static double radius = 0.05;
  const double delta_theta = pi2/20;
  double xcenter , ycenter;  
  double x, y;
  double theta = 0.0;

  double current_angle = cos(omega * time);

  glColor3f(0.0, 0.0, 0.0);
  glClear(GL_COLOR_BUFFER_BIT);
  glColor3f(1.0, 1.0, 1.0);

  /* Draw pendulum cord */  
  glColor3f(1.0, 1.0, 1.0);
  glBegin(GL_LINES);
  glVertex2f(0.0, 0.0);
  xcenter = -cord_length * sin(current_angle);
  ycenter = -cord_length * cos(current_angle);
  glVertex2f(xcenter, ycenter);
  glEnd();

  /* Draw pendulum dish */
  glColor3f(1.0, 0.0, 0.0);
  glBegin(GL_POLYGON);
  while (theta <= pi2) {
    x = xcenter + radius * sin(theta);
    y = ycenter + radius * cos(theta);
    glVertex2f(x, y);
    theta += delta_theta;
  };
  glEnd();
  
  glutSwapBuffers();
};

Aufgaben

Hier sind einige Vorschläge, wie der Leser den bisher gelernten Stoff trainieren und verinnerlichen kann:

Ausblick

Das wars für dieses Mal. Es gibt noch Vieles über Polygone zu sagen. In der nächsten Ausgabe (März 1998) werden weiterhin die Polygone erforscht und wird detailierter auf die bereits bekannten Befehle eingegangen.

Literaturverweise