![[LinuxFocus Image]](../../common/January1998/border-short.jpg)
| Noticias Archivos Compañias Consejos y Trucos |
Programando OpenGL: Trazado de Polígonos Simplespor Miguel Angel Sepúlveda |
Introducción
Dibujando Puntos
Dibujando Lineas y Polígonos
Ejercicios
Proximamente
IntroducciónEste es el primer artículo de una serie sobre OpenGL, un estándar de la industria para gráficos 2D/3D (ver también Qué es OpenGL). Supondremos que el lector está familiarizado con su plataforma de desarrollo en C, y que tiene ciertos conocimientos con la librería GLUT (sinó, puedes seguir la serie de artículos "Programando GLUT" en este magazine). Bajo Linux, recomendamos el uso de la librería Mesa, que es una maravillosa implementación freeware de OpenGL. Actualmente existe incluso soporte hardware para Mesa (ver Tarjetas gráficas 3Dfx).
La presenación de cada nuevo comando de OpenGL vendrá acompañada de un ejemplo que trata de utilizar su funcionalidad, ¡por lo menos lo intentaremos!. Hacia el final de nuestra serie, os mostraremos el código fuente de un juego de simulación escrito completamente en OpenGL.
Antes de empezar, me gustaría mencionar que, como científico, la mayor parte de mi experiencia con OpenGL proviene de utilizarlo como herramienta para escribir simulaciones de sistemas clásicos y reales. Así pues, todos mis ejemplos van sobre eso ;-). Espero que los lectores encuentren estos ejemplos accesibles o, al menos, divertidos. Si te gustaría ver otro tipo de ejemplos, házmelo saber.
OpenGL se asocia a menudo con gráficos 3D, fantásticos efectos especiales, modelos complejos con modelado realístico de luces, etc. Sin embargo, también es una máquina de trazado de gráficos 2D. Esto es importante porque hay muchas cosas que puedes aprender a hacer en 2D antes de aprender las complejidades de las perspectivas 3D, el trazado de modelos, luces, posiciones de cámaras, etc. Un gran número de aplicaciones de ingeniería y ciencias se pueden trazar en 2D. Así pues, aprendamos primero cómo hacer sencillas animaciones en 2D. Dibujando PuntosOpenGL tiene únicamente unas pocas primitivas geométricas: puntos, líneas, polígonos. Todas ellas se describen en términos de sus respectivos vértices. Un vértice está caracterizado por 2 o 3 números en como flotante, las coordenadas cartesianas del vértice, (x, y) en 2D y (x, y, z) en 3D. Aunque las coordenadas cartesianas son las más comunes, en gráficos por ordenador también existe el sistema coordenado homogéneo en el que cada punto se describe con 4 números en coma flotante (x, y, z, w). Volveremos a él después de ver algunas nociones elementales de trazado en 3D. Como en OpenGL todos los objetos geométricos son finalmente descritos como un conjunto ordenado de vértices, existe una familia de rutinas para declarar un vértice en OpenGL, su sintaxis es: void glVertex{234}{sifd}[v](TYPE coords);Familiarízate con esta notación. Las llaves indican parte del nombre de la rutina, las rutinas pueden tomar 2, 3 o 4 parámetros de tipo short, long, float o double. Opcionalmente, estos parámetros se pueden proporcionar en forma de vector, en este caso deberemos usar la rutinas del tipo v. Aquí hay algunos ejemplos: void glVertex2s(1, 3);void glVertex2i(23L, 43L); void glVertex3f(1.0F, 1.0F, 5.87220972F); float vector[3]; void glVertex3fv(vector); Para simplificar nos referiremos a estas rutinas como glVertex*. OpenGL interpreta cualquier secuencia de vértices segú:n su contexto. El contexto se declara mediante el par de rutinas glBegin(GLenum mode) y glEnd(), toda sentencia glVertex* ejecutada entre estas dos se interpreta según el valor de mode, por ejemplo: glBegin(GL_POINTS);glVertex2f(0.0, 0.0); glVertex2f(1.0, 0.0); glVertex2f(0.0, 1.0); glVertex2f(1.0, 1.0); glVertex2f(0.5, 0.5); glEnd(); dibuja 5 puntos en 2D con las coordenadas especificadas. GL_POINTS es una de las etiquetas definidas en el fichero cabecera de OpenGL <GL/gl.h>, existen muchos otros modos disponibles, pero los veremos cuando sea necesario. Cada punto se dibuja con el color actualmente guardado en la variable de estado de OpenGL asociada con el buffer de color. Para cambiar el color actual, usaremos la familia de rutinas glColor*; hay mucho que decir sobre la selección y manipulación de colores, habrá un artículo solo para esto. De momento podemos utilizar tres números en coma flotante entre 0.0 y 1.0. Es el codificado RGB (rojo-verde-azul) glColor3f(1.0, 1.0, 1.0); /* Blanco */glColor3f(1.0, 0.0, 0.0); /* Rojo */ glColor3f(1.0, 1.0, 0.0); /* Magenta */ etc... ../../common/January1998/Makefile ../../common/January1998/../../common/January1998/example1.c ../../common/January1998/../../common/January1998/example2.c Ya tenemos suficiente material para escribir nuestros dos primeros
ejemplos de código. El primer ejemplo es un simple programa en OpenGL que
dibuja un número de órbitas de una transformación
caótica (la transformación
estandar). Si el lector no está familiarizado con transformaciones
y con la transformación estandar en particular, no importa. Dicho
sencillamente, la transformación toma un punto y genera uno nuevo usando
una fórmula definida como: Este es el código de ../../common/January1998/../../common/January1998/example1.c:
#include <GL/glut.h>
#include <math.h>
const double pi2 = 6.28318530718;
void NonlinearMap(double *x, double *y){
static double K = 1.04295;
*y += K * sin(*x);
*x += *y;
*x = fmod(*x, pi2);
if (*x < 0.0) *x += pi2;
};
void winInit(){
/* Poner sistema de coordenadas */
gluOrtho2D(0.0, pi2, 0.0, pi2);
};
void display(void){
const int NumberSteps = 1000;
const int NumberOrbits = 100;
const double Delta_x = pi2/(NumberOrbits-1);
int step, orbit;
glColor3f(0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
y = 3.1415;
x = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
x = 3.1415;
y = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
};
int main(int argc, char **argv) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);
glutInitWindowPosition(5,5);
glutInitWindowSize(300,300);
glutCreateWindow("Standard Map");
winInit();
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Léete el artículo Programando GLUT para entender las rutinas glut*, la mayor parte de este código viene de ahí. La ventana gráfica se abre en modo buffer simple y RGB. Entonces una función callback llamada display() dibuja la transformación: primero seleccionamos el color negro para el fondo y glClear(GL_COLOR_BUFFER_BIT) pone el buffer de color al color actual (negro), a continuación, después de seleccionar el color blanco con glColor, ejecutamos unas cuantas veces la función NonlinearMap() y dibujamos los puntos con glVertex* en modo GL_POINTS. Realmente simple. Fíjate con en la rutina de inicialización de la ventana winInit() hay una única instrucción del toolkit de utilidades de OpenGL, gluOrtho2D(). Esta rutina pone un sistema de coordenadas 2D ortogonal. Los parámetros que recibe son "mínimo x, máximo x, mínimo y, máximo y". He elgido una ventana en modo simple y un gran número de puntos para que puedas ver la imagen mientras es dibujada. Esto es habitual en modo simple con imágenes grandes y que tarden en calcularse, los dibujos aparecen en pantalla tal y como van siendo generados por las rutinas de OpenGL. Después de ejecutar ../../common/January1998/example1 deberías ver esta imagen:  Vayamos al segundo programa, ../../common/January1998/../../common/January1998/example2.c:
#include <GL/glut.h>
#include <math.h>
const double pi2 = 6.28318530718;
const double K_max = 3.5;
const double K_min = 0.1;
static double Delta_K = 0.01;
static double K = 0.1;
void NonlinearMap(double *x, double *y){
/* Transformación estandar */
*y += K * sin(*x);
*x += *y;
/* El ángulo x es módulo 2Pi */
*x = fmod(*x, pi2);
if (*x < 0.0) *x += pi2;
};
/* Función callback:
Qué hacer en ausencia de entradas */
void idle(void){
/* Incrementar el parámetro estocástico */
K += Delta_K;
if(K > K_max) K = K_min;
/* Redibujar el display */
glutPostRedisplay();
};
/* Inicialización de la ventana gráfica */
void winInit(void){
gluOrtho2D(0.0, pi2, 0.0, pi2);
};
/* Función callback:
Qué hacer cuando el display se ha de redibujar */
void display(void){
const int NumberSteps = 1000;
const int NumberOrbits = 50;
const double Delta_x = pi2/(NumberOrbits-1);
int step, orbit;
glColor3f(0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
y = 3.1415;
x = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
x = 3.1415;
y = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
glutSwapBuffers();
};
int main(int argc, char **argv) {
/* Inicializaciones de GLUT */
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA);
glutInitWindowPosition(5,5);
glutInitWindowSize(300,300);
/* Abrir ventana*/
glutCreateWindow("Order to Chaos");
/* Inicialización de la ventana */
winInit();
/* Registrar funciones callback */
glutDisplayFunc(display);
glutIdleFunc(idle);
/* Iniciar el proceso de eventos */
glutMainLoop();
return 0;
}
Este programa se basa en ../../common/January1998/../../common/January1998/example1.c, la principal diferencia es que la ventana se abre en modo de doble buffer, y el parámetro K de la transformación es una variable que cambia durante la ejecución del programa. Hay una nueva función callback idle() registrada para el procesador de eventos de GLUT por glutIdleFunc().Esta función tiene un significado especial, es ejecutada por el procesador de eventos en todo momento que no hay entrada del usuario. La función callback idle() es ideal para animaciones de programas. En ../../common/January1998/example2, se utiliza para cambiar ligeramente el valor del parámetro de la transformación. Al final de idle() hay otra función de GLUT útil, glutPostResDisplay() que redibuja la ventana conservando la inicializaciones anteriores, en general es más eficiente que llamar a display() de nuevo. Otra diferencia a señalar es el uso de glutSwapBuffers() al final de display(). La ventana se inició en modo doble buffer por lo que todas las directivas de trazado se aplican al buffer oculto, el usuario no ve cómo se dibuja la imagen en este caso. Cuando se ha finalizado la imagen completa (frame), entonces se hace visible intercambiando los buffers visible e invisible con glutSwapBuffers(). Sin esta técnica la animación no iría suave. Estas son algunas imágenes que se ven durante la animación:  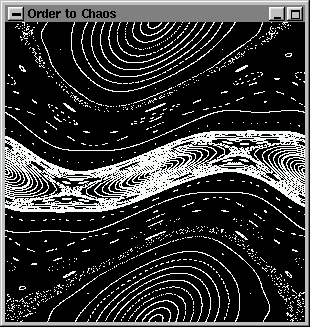  IMPORTANTE: LA función callback display() siempre se invoca al menos una vez antes que idle(). Recuerda esto cuando escribas tus animaciones y decidas qué va en display() y qué va en idle(). ../../common/January1998/../../common/January1998/example3.c Dibujando Líneas y PolígonosComo hemos dicho antes, glBegin(GLenum mode) acepta varios modos, y la secuencia de vértices v0, v1,v2, v3,v4,... vn-1 declarados a continuación se interpreta acordemente. Los valores posibles para mode y su significado son:
En nuestro tercer ejemplo, otra animación, hacemos uso de GL_LINES y GL_POLYGON. Compila el programa, mírate el código fuente y observa cómo funciona. Es básicamente muy similar a ../../common/January1998/../../common/January1998/example2.c, ahora la imagen dibujada es un péndulo muy simple. La animación simula el movimiento de un péndulo ideal. Esto es una fotografía de la animación: 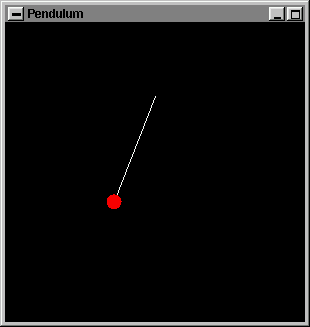 Como antes, hay una función callback idle() cuya misión aquí es mantener el reloj funcionando (actualizando la variable time). La función display() dibuja dos objetos, la cuerda del péndulo y su peso (en blanco y rojo respectivamente). El movimiento de las coordenadas del péndulo está implícito en las fórmulas de xcenter y ycenter:
void display(void){
static double radius = 0.05;
const double delta_theta = pi2/20;
double xcenter , ycenter;
double x, y;
double theta = 0.0;
double current_angle = cos(omega * time);
glColor3f(0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
/* Dibujar la cuerda del péndulo */
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINES);
glVertex2f(0.0, 0.0);
xcenter = -cord_length * sin(current_angle);
ycenter = -cord_length * cos(current_angle);
glVertex2f(xcenter, ycenter);
glEnd();
/* Dibujar el disco del péndulo */
glColor3f(1.0, 0.0, 0.0);
glBegin(GL_POLYGON);
while (theta <= pi2) {
x = xcenter + radius * sin(theta);
y = ycenter + radius * cos(theta);
glVertex2f(x, y);
theta += delta_theta;
};
glEnd();
glutSwapBuffers();
};
EjerciciosAquí te damos algunas sugerencias para que practiques lo que has aprendido hasta ahora:
Proximamente....Esto es todo de momento. Hay todavía muchas cosas a discutir sobre polígonos. En el próximo número (Marzo 1998) continuaremos explorando los polígonos, modelado y estudiaremos más detalles sobre algunos de los comandos que ya nos son familiares. |
Traducido por Hugo Lastras
- Lea La Tarjeta Gráfica 3Dfx.
- Consulte http://www.opengl.org/.
- Otros artículos por el mismo autor:Qué es OpenGL?, Programando GLUT: Ventanas y Animaciones.
Esta página está mantenida por Miguel A Sepulveda.